#harmonic analysis
This is the second of two posts based on a talk given at Dmitriy Bilyk at our probability seminar (the first one is here). I don’t usually go to probability seminar, but have enjoyed Dmitriy’s talks in the past, and I didn’t regret it this time either :)
——
Semirandom Methods
In the previous post we defined the Riesz energy and the discrepancy, and we said that (deterministic!) sets which minimize either of these things should be said to be “uniformly distributed”. We also mentioned that in general, we don’t know very many deterministic methods for creating uniformly distributed points on the sphere.
Using these two measures, the situation does not improve much for purely deterministic methods. But it turns out that there are two semirandom methods that do pretty well by both measures. The easiest to describe, and the most successful, is called jittered sampling: take one point uniformly at random from each part of any “regular equal-area partition”, which is some technical thing that’s not important. What’s important are the results:
- It on average achieves the upper bound in Beck’s theorem of $\approx N^{-\frac12-\frac1{2d}}\sqrt{\log N}$.
- It doesn’t optimize the Riesz energies, but it “almost” does so, in a way that Bilyk did not describe.
Somewhat more complicated is the determinental point process. It seems that nowadays these are of pretty big interest to machine learning, idk. But I do know (or rather, Bilyk knows and so I can inform you) that it enjoys similar properties to jittered sampling, although it is not quite as good in the discrepancy sense (I believe it’s $\log N$ instead of $\sqrt{\log N}$, but don’t quote me).
He also talked about some work that he did with Feng Dai and my colleague and friend Ryan Matzke related to the Stolarsky Invariance Principle. I think this produces a third semirandom method which has similarly nice properties, although to be honest I did not really follow that part of the talk >.>
However, there has recently been a new theoretical advance which has allowed for the possibility of more deterministic methods; we’ll spend the rest of the post talking abut that.
——
Uniform Tessellations
Given two points $x$ and $y$ on the sphere, and a random hyperplane, the probability that the hyperplane separates them is the spherical distance between them $d(x,y)$ [technicality: on a sphere of appropriate radius such that the distance from the north to the south pole is $1$]. Motivated by this fact, we define a Hamming distance, relative to a given set $Z=\{z_1,\dots, z_N\}$, between two points $x$ and $y$ as
$$ d_Z(x,y) = \frac{\#\{z_i\in Z: z_i^\perp \text{ separates }x\text{ from } y\}}{N}.$$
[ Those of you who know a different notion of Hamming distance may be interested in reading Section 1.1 of this paper, which lays out the relationship very clearly. ]
For any fixed $x$ and $y$, as $N\to\infty$, the expected Hamming distance (over all sets of size $N$) converges to $d(x,y)$; this says that the Hamming distance is a fairly reasonable object. But what we actually want to do is the following: for any set $X\subset S^d$ (which need not be finite), we say that $Z$ induces a $\delta$-uniform tessellation of $X$ in the event that $\sup_X |d_Z(x,y)-d(x,y)| \leq \delta$.
The goal is to find small $N$ which admit sets that induce $\delta$-uniform tessellations of $X$; ideally the smallest such $N$. Of course finding large $N$ is not very hard: as the number of hyperplanes grows, there will eventually be some set which does this. Indeed, the existence of $\delta$-uniform tessellations can be understood as “speed of convergence” results for the convergence $d_Z\to d$ mentioned above.
Of course the answer is going to have to depend somehow on the geometry of $X$, and so our answer is going to have to depend on some quantified statement of how “bad” the geometry is. I do not wish to explain exactly how this is done, but Bilyk and Lacey were able to come up with two answers:
Theorem (Bilyk–Lacey). There exist constants $C$ and $C’$ such that it is sufficient for either $N\geq C\delta^{-3}\omega(X)$, or $N\geq C’\delta^{-2}H(X)$.
Here, $\omega(X)$ is a classically studied geometric statistic, and $H(X)$ is a variant which Bilyk and Lacey invented.
This dramatically improves on previous results, and in particular gets us tantalizingly close to the (previously) conjectured optimal lower bound, which is $C\delta^{-2}\omega(X)$. You can see that this conjecture is sort of the combination of their two results: it takes the $-2$ power from the second bound but still uses the $\omega$ statistic. Unfortunately, Bilyk did not seem optimistic that there were many technical improvements that could be made to their idea. So breaking the $-3$ barrier with the $\omega$ is probably still in want of another innovation.
This is the first of two posts based on a talk given at Dmitriy Bilyk at our probability seminar. I don’t usually go to probability seminar, but have enjoyed Dmitriy’s talks in the past, and I didn’t regret it this time either :)
——
Unsatisfactory Methods
Here is how not to pick a point uniformly on the sphere: don’t pick its polar and azimuthal angles uniformly. This doesn’t work because it will incorrectly bias things toward the poles.
What does work is to pick the polar angle and $z$-coordinateuniformly.
So that was a short talk :P
The problem is that this cylindrical trick only works on the 2-sphere. There is no natural notion of “cylindrical coordinates” for higher-dimensional spheres, because how many coordinates do you take linearly and how many do you take as angles?
Bilyk did not say this, but presumably no choice you can make, or at least no consistent choices that you can make for all $n$, such that you get a uniform distribution— otherwise it really would have been a short talk :P
What Bilyk did say is that there are several ways to choose points uniformly from a sphere, but “there are very few deterministic methods”. But before we can tackle these methods, we actually need to answer a more fundamental question: what does it mean to choose deterministically choose points uniformly? Generally “choosing uniformly” means sampling from a constant random variable, but that X is clearly not available to us here.
——
Riesz Energy
One way to go might be to minimize the Riesz energy. Whenever we have a collection of points $Z=\{z_1,\cdots z_N\}$, can write
$$ E_s = \frac{1}{N^2} \sum_i \sum_{j\neq i} \frac{1}{z_i-z_j}. $$
We see that if the $z_k$ are very close to each other, this energy is going to be large; a set $Z$ that makes the energy small will be one whose points are generally “as far from each other as possible”. Since it’s a sphere, you can’t get too far away, and so there’s an interesting optimization to be done here.
So this seems nice, but there’s a problem. It turns out that minimizing the Riesz energy is just, like, stupendously hard. The best exact result we have was given in 2010, when Schwartz proved that $E_1$ is minimized for $N=5$ (!) by the triangular bipyramid.

(source)
To give some indication about why the problem is hard: the triangular bipyramid is not the minimizer for the Riesz energy with $N=5$ for all $s$. It is suspected that it minimizes it for all sufficiently small $s$; but one thing we know for sure that when $s$ gets large enough, the square pyramid is better.
Conjecture. There exists a critical value $s’$ such that for all $1\leq s<s’$, the triangular bipyramid minimizes $E_s$, and for all $s’<s$, the square pyramid minimizes $E_s$.
This conjecture is wide open: we don’t even know that the square pyramid minimizes $E_s$ for any value of $s$!
——
Discrepancy and a Theorem of Beck
Another, rather different way to measure the uniform-ness of a set $Z$ is by computing its discrepancy. The formal definition of discrepancy is really a lot scarier than necessary, so I won’t write it here. The idea is that if you pick any (measurable) set $S$, you can either
- calculate the measure of the $S$, or
- count how many of the points $z_i$ live inside $S$
Most of the time, these two numbers are going to be different, and the discrepancy $D(Z,S)$ is the difference between the numbers, divided by the number of points in $Z$. But this is not the most useful number because we have this extra data $S$ hanging around; the better idea is to let the discrepancy be the maximum of $D(Z,S)$ over all $S$ (technically the supremum).
Intuitively speaking, that if you were to have a $Z$ for which the discrepancy in the latter sense were small, then $Z$ looks “uniformly distributed”, even if $Z$ is deterministic.
However, measurable sets can look pretty wacky, and so in order to let geometry reign over set theory, it often helps to be a little more refined. Given a collection of sets $\mathcal S$, we say that the discrepancy $D(Z,\mathcal S)$ is the supremum of $D(Z,S)$ over all $S\in\mathcal S$. So it’s basically the same thing as what we did above, except that instead of doing all measurable sets, we only do the ones in the collection.
Figuring out optimal discrepancies is also not very easy, but people have over the years figured out strategies for determining asymptotic bounds. And even that tends to be pretty tough. For instance, if we’re considering things on the sphere, it may seem reasonable to look at $\mathcal S$ the collection of spherical caps:
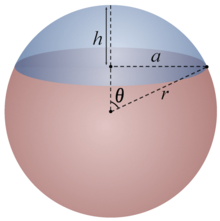
(source)
What is the best available discrepancy in this setting? The answer, morally speaking, is that it’s “close to $1/\sqrt{N}$”, but it has a small dimensional correction:
Theorem (Beck 1984). For any positive integer $N$, there exist positive constants $C_0$ and $C_1$ such that
$$ C_0 N^{-\frac12-\frac1{2d}} \leq \inf_{|Z|=N} D(Z,\mathcal S) \leq C_1 N^{-\frac12-\frac1{2d}} \sqrt{\log N}, $$
where $\mathcal S$ is the set of spherical caps.
So you can always find a set $Z$ that does a little better, asymptotically, than $1/\sqrt{N}$; what exactly “a little” means depends on how high-dimensional your sphere is.
——
In the next post, we talk about more recent developments, including a third notion of uniform distribution which will bring us all the way to Bilyk’s work in the present day.
