#category theory
This post represents the second half of a talk given by Emine Yildirim at our combinatorics seminar.
If you’ve not already read the first one, you don’t technically have to, as long as you’re happy assuming that there are special posets associated to each Coxeter group called “cominiscule”. But it will probably be more rewarding if you read the posts in order.
In any case, this post will make really no attempt at all to be elementary.
——
Excuse Me, Which Algebra?
We wish to consider a path algebra, and so we need to have a directed graph. You might imagine that we would just use the Hasse diagrams of the posets which we just drew, with some orientation thrown on. That’s a very reasonable guess; it just happens to not be what Yildirim did.
Instead she first considers the set of order ideals (which are all subsets of poset elements which are “downward closed”: if $x$ is in the subset then every $a\leq x$ must also be in the subset) of a cominiscule poset. Since order ideals are, in particular, subsets of the same set, the collection of all order ideals come with their own natural order structure— namely, inclusion of sets.
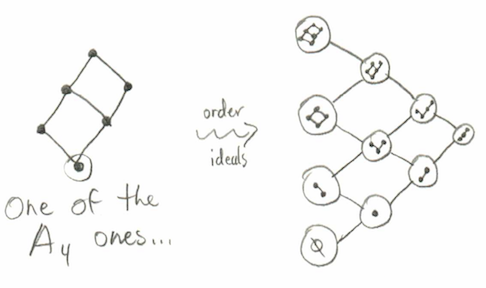
[ Eagle-eyed viewers may notice what one of the members of the audience pointed out: this poset structure is actually a cominiscule poset itself (for type C). After some consideration, we decided that this is probably a coincidence; the order ideal poset of cominiscule posets will not in general be cominiscule. ]
We take the Hasse diagram of that poset (e.g. as drawn above), interpret it as a graph with the edges as directed downward, and finally take the path algebra of that(whew!). We will call such an algebra $\mathcal A$, suppressing the dependence on the cominiscule root. Note that this directed graph is acyclic, and so $\mathcal A$ is finite-dimensional.
In any case, the goal is to prove the following:
Conjecture. The Auslander-Reiten translation $\tau$ has finite order $2(h+1)$ on the Grothendeick group of the bounded derived category of $\textbf{Mod}(\mathcal A)$.
So there’s lots of words here but the point is that that Yildirim was able to prove this conjecture for all the cominiscule posets… except the triangular poset that comes from types C and D. So it’s technically still a conjecture, but she solved a substantial portion of it, and so I will still refer to “Yildirim’s proof.”
In the remainder of the post, we make an attempt to explain why this might be true, and why the Coxeter transformation has anything to do with anything.
——
“Bounded Derived Category”?
I will not attempt to define the bounded derived category construction, but I will tell you an important fact abut it: it is “derived” in the sense that its objects are chain complexes $\to A \to B\to C\to$, but all of the quasi-isomorphisms are invertible.
This bit of abstract nonsense means that we can replace any $\mathcal A$-module $M$ by its minimal projective resolution:
$$ 0 \to P_{n}\to \cdots \to P_{2}\to P_{1}\to P_{0} \to 0. $$
[ Here we are using the “homological” definition of a projective resolution, where $M$ does not show up in the sequence itself but rather is isomorphic to the kernel of the last map. It’s not super important. ]
In the post based on Yildirim’s pre-talk, we pointed out that the defining characteristic of the Coxeter transformation is that it “turns projectives into injectives”. One can define the Coxeter transformation so that it does this functorially, i.e. in such a way that we get a sequence
$$ 0 \to I_{n}\to \cdots \to I_{2}\to I_{1}\to I_{0} \to 0. $$
This turns out to be an injective coresolution of any module $N$ (“co” meaning that $N$ is the of the kernel of the second map), and we say that the Coxeter transformation turns $M$ into $N$.
Update: actually things are even worse than I thought: in general this does not even have to be an injective resolution! (Thanks @yildirimemine (!!) for the correction.)
——
The Key Lemma
The Coxeter transformation is a useful tool for understanding the Auslander-Reiten translation $\tau$, but there is a major hurdle to making it any more useful than just using $\tau$ itself.
A module $M$ of a path algebra coming from a Hasse diagram is called an interval if it arises as a quiver representation in the following way:
- choose an “upper” vertex $\beta$ and a “lower” vertex $\alpha\leq\beta$,
- for each vertex $v$ between these two, i.e. satisfying $\alpha\leq v\leq\beta$, place a copy of the field $k$ at $v$, and
- place the zero map at every edge between any two vertices.
Then the Coxeter transformation need not take intervals to intervals.
However, Yildirim’s proof of the conjecture relies on the following discovery.
Lemma. For all $\mathcal A$ except the one arising from the triangular poset, there exists a collection of intervals which are taken to intervals. Moreover, these form a basis for the (relevant) Grothendieck group.
Again these are words, but they have a practical effect. Namely, any module $M$ can be broken down into pieces, each of which is an interval that is taken to an interval. So, roughly speaking, as long as we understand the Coxeter transformation on such modules, we understand the Coxeter relation in general.
[ In light of the Update, this becomes even more remarkable: some intervals are not even taken to resolutions! And yet somehow there is this nice collection we can carve out that not only is taken to resolutions, but even resolutions of intervals…]
Because of this, and because of the Coxeter transformation’s close connection to the Auslander-Reiten translation, she is able to understand the latter in a more stripped-down form, without its full algebraic trappings. This, finally, she uses to prove the conjecture. The difficulty with the single remaining family of posets is that we do not (yet?) have such a basis.
[Previous ] [ Post 3 ]

