#combinatorics
Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - VI

(continued from here)
“O Oysters, come and walk with us!” The Walrus did beseech. “A pleasant walk, a pleasant talk, Along the briny beach: We cannot do with more than four, To give a hand to each.”
* * *
“The time has come,” the Walrus said, “To talk of many things: Of shoes–and ships–and sealing-wax– Of cabbages–and kings– And why the sea is boiling hot– And whether pigs have wings.”
-Lewis Carroll, The Walrus and the Carpenter

In this segment, probable numbers will be shown to grow out of a natural context inherently rather than through geometric second thought as transpired in the history of Western thought with imaginary numbers and complex plane. To continue with development of probable numbers it will be necessary to leave behind, for the time being, all preoccupation with imaginary numbers and complex plane. It will also be necessary to depart from our comfort zone of Cartesian spatial coordinate axioms and orientation.
Probable coordinates do not negate validity of Cartesian coordinates but they do relegate them to the status of a special case. In the probable coordinate system the three-dimensional coordinate system of Descartes maps only one eighth of the totality. This means then, that the Cartesian two-dimensional coordinate plane furnishes just one quarter of the total number of corresponding probable coordinate mappings projected to a two-dimensional space.[1] It suggests also that Cartesian localization in 2-space or 3-space is just a small part of the whole story regarding actual spatial and temporal locality and their accompanying physical capacities, say for instance of momentum or mass, but actually encompassing a host of other competencies as well.
Although this might seem strange it is a good thing. Why is it a good thing? First, because nature, as a self-sustaining reality, cannot favor any one coordinate scheme but must encompass all possible - if it is to realize any. Second, because both the Schrödinger equationandFeynman path integral approaches to quantum mechanics say it is so.[2] Third, because Hilbert space demands it. This may leave us disoriented and bewildered, but nature revels in this plan of probable planes. Who are we to argue?
So how do we accomplish this feat? Well, basically by reflections in all dimensions and directions. We extend the Cartesian vectors every way possible. That would give us a 3 x 3 grid or lattice of coordinate systems (the original Cartesian system and eight new grid elements surrounding it), but there are only four different types, so we require only four of the nine to demonstrate. It is best not to show all nine in any case because to do so would place our Cartesian system at direct center of this geometric probable universe and that would be misleading. Why? Because when we tile the two-dimensional universe to infinity in all directions, there is no central coordinate system. Any one of the four could be considered at the center, so none actually is. Overall orientation is nondiscriminative.[3]
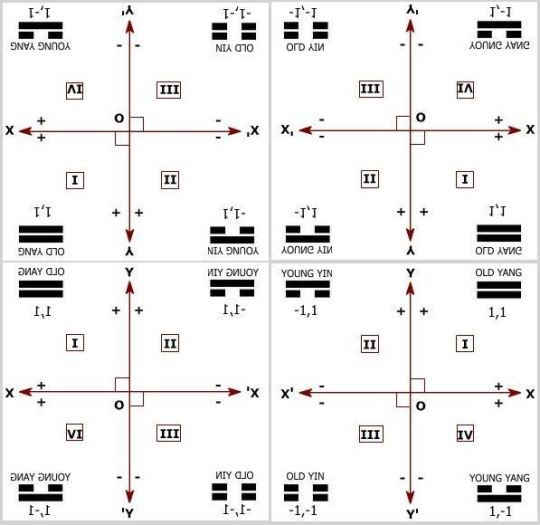
LOOKING GLASS CARTESIAN COORDINATE QUARTET
The image seen immediately above shows four Looking House Cartesian coordinate systems, correlated within a mandalic plane. This mandalic plane is one of six faces of a mandalic cube, each of which is constructed to a different plan but composed of similar building blocks, the four bigrams in various positions and orientations. A 2-dimensional geometric universe can be tiled with this image, recursively repeating it in all directions throughout the two dimensions.[4] It should not be very difficult for the reader to determine which of the four mandalic moieties references our particular conventional Cartesian geometric universe.[5]

It remains only to be added here and now that potential dimensions, probable planes, and probable numbers arise immediately and directly from the remarks above. In some ways it’s a little like valence in chemical reactions. We’ll likely take a look at that combinatory dynamic in context of mandalic geometry at some time down the road. Next though we want to see how the addition of composite dimension impacts and modifies the basic geometry of the probable plane discussed here.[6]
(to be continued)
Top image: The four quadrants of the Cartesian plane. These are numbered in the counterclockwise direction by convention. Architectonically, two number lines are placed together, one going left-right and the other going up-down to provide context for the two-dimensional plane. This image has been modified from one found here.
Notes
[1] To clarify further: There are eight possible Cartesian-like orientation variants in mandalic space arranged around a single point at which they are all tangent to one another. If we consider just the planar aspects of mandalic space, there are four possible Cartesian-like orientation variants which are organized about a central shared point in a manner similar to how quadrants are symmetrically arranged about the Cartesian origin point (0,0) in ordinary 2D space. But here the center point determining symmetries is always one of the points showing greatest rather than least differentiation. That is to say it is formed by Cartesian vertices, ordered pairs having all 1s, no zeros. That may have confused more than clarified, but it seemed important to say. We will be expanding on these thoughts in posts to come. Don’t despair. For just now the important takeaway is that the mandalic coordinate system combines two very important elements that optimize it for quantum application: it manages to be both probabilistic and convention-free (in terms of spatial orientation, which surely must relate to quantum states and numbers in some as yet undetermined manner.) At the same time, imaginary numbers and complex plane are neither.
[2] Even if physics doesn’t yet (circa 2016) realize this to be true.
[3] It is an easy enough matter to extrapolate this mentally to encompass the Cartesian three-dimensional coordinate system but somewhat difficult to demonstrate in two dimensions. So we’ll persevere with a two-dimensional exposition for the time being. It only needs to be clarified here that the three-dimensional realization involves a 3 x 3 x 3 grid but requires just eight cubes to demonstrate because there are only eight different coordinate system types.
[4] I am speaking here in terms of ordinary dimensions but it should be understood that the reality is that the mandalic plane is a composite 4D/2D geometric structure, and the mandalic cube is a composite 6D/3D structure. The image seen here does not fully clarify that because it does not yet take into account composite dimension nor place the bigrams in holistic context within tetragrams and hexagrams. All that is still to come. Greater context will make clear how composite dimension works and why it makes eminent good sense for a self-organizing universe to invoke it. Hint: it has to do with quantum interference phenomena and is what makes all process possible.
ADDENDUM (12 APRIL, 2016)
The mandalic plane I am referring to here corresponds to the Cartesian 2-dimensional plane and is based on four extraordinary dimensions that are composited to the ordinary two dimensions, hence hybrid 4D/2D. It should be understood though that any number of extra dimensions could potentially be composited to two or three ordinary dimensions. The probable plane described in this post is not such a mandalic plane as no compositing of dimensions has yet been performed. What is illustrated here is an ordinary 2-dimensional plane that has undergone reflections in x- and y-dimensions of first and second order to form a noncomposited probable plane. The distinction is an important one.
[5] This is perhaps a good place to mention that the six planar faces of the mandalic cube fit together seamlessly in 3-space, all mediated by the common shared central point, in Cartesian terms the origin at ordered triad (0.0.0) where eight hexagrams coexist in mandalic space. Moreover the six planes fit together mutually by means of a nuclear particle-and-force equivalent of the mortise and tenon joint but in six dimensions rather than two or three, and both positive and negative directions for each.
[6] It should also be avowed that tessellation of a geometric universe with a nondiscriminative, convention-free coordinate system need not exclude use of Cartesian coordinates entirely in all contextual usages. Where useful they can still be applied in combination with mandalic coordinates since the two can be made commensurate, irrespective of specific Cartesian coordinate orientation locally operative. Whatever the Cartesian orientation might be it can always be overlaid with our conventional version of the same. More concretely, hexagram Lines can be annotated with an ordinal numerical subscript specifying Cartesian location in terms of our local convention should it prove necessary or desirable to do so for whatever reason.
On the other hand, before prematurely throwing out the baby with the bath water, we might do well to ask ourselves whether these strange juxtapositions of coordinates might not in fact encode the long sought-after hidden variables that could transform quantum mechanics into a complete theory. In mandalic coordinates of the reflexive nature described, these so-called hidden variables could be hiding in plain sight. Were that to prove the case, David Bohm andLouis de Broglie would be immediately and hugely vindicated in advancing their pilot-wave theory of quantum mechanics. We could finally consign the Copenhagen Interpretation to the scrapheap where it belongs, along with both imaginary numbers and the complex plane.
ADDENDUM (24 APRIL, 2016)
Since writing this I’ve learned that de Broglie disavowed Bohm’s pilot wave theory upon learning of it in 1952. Bohm had derived his interpretation of QM from de Broglie’s original interpretation but de Broglie himself subsequently converted to Niels Bohr’s prevailing Copenhagen interpretation.
© 2016 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 311-
Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - IV
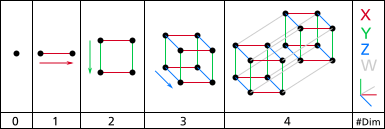
(continued from here)
One of the notable things the Rationalists failed to take into account in their analysis and codification of square roots was the significance of context. In so doing they assured that all related concepts they developed would eventually degenerate into a series of errors of conflation. Do not ever underestimate the importance of context.
Mathematicians, for example, can show that for any 3-dimensional cube there exists a 2-dimensional square, the area of which equals the volume of the cube.[1] And although that is true, something has been lost in translation. This is another of the sleights of hand mathematicians are so fond of. Physicists cannot afford to participate in such parlor tricks as these, however mathematically true they might be.[2]
We will begin now, then, to examine how the mandalic coordinate approach stacks up against that of imaginary numbers and quaternions. The former are holistic and respective of the natural order; the latter are irresponsibly rational, simplistic and, in final analysis, wrong about how nature works.[3] Ambitious endeavor indeed, but let’s give it a go.
We’ve already looked at how the standard geometric interpretation of imaginary numbers in context of the complex plane is based on rotations through continuous Euclidean space. You can brush up on that aspect of the story here if necessary. The mandalic approach to mapping of space is more complicated and far more interesting. It involves multidimensional placement of elements in a discrete space, which is to say a discontinuous space, but one fully commensurate with both Euclidean and Cartesian 3-dimensional space. The holo-interactive manner in which these elements relate to one another leads to a probabilistic mathematical design which preserves commutative multiplication, unlike quaternions which forsake it.
Transformations between these elements are based on inversion (reflection through a point) rather than rotation which cannot in any case reasonably apply to discrete spaces. The spaces that quantum mechanics inhabits are decidedly discrete. They cannot be accurately detailed using imaginary and complex numbers or quaternions. To discern the various, myriad transitions which can occur among mandalic coordinates requires some patience. I think it cannot be accomplished overnight but at least in the post next up we can make a start.[4]
(continuedhere)
Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions (A tesseract). There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons
Notes
[1] If only in terms of scalar magnitude. Lost in translation are all the details relating to vectors and dimensions in the original. Conflation does not itself in every case involve what might be termed ‘error’ but because it always involves loss or distortion of information, it is nearly always guaranteed to eventuate in error somewhere down the line of argument. The point of all this in our context here is that, in the history of mathematics, something of this sort occurred when the Rationalists of the Enlightenment invented imaginary and complex numbers and again when quaternions were invented in 1843. These involved a disruption of vectors and dimensions as treated by nature. The loss of information involved goes a long way in explaining why no one has been able to explain whyandhow quantum mechanics works in a century or more. These misconstrued theses of mathematics behave like a demon or ghost in the machine that misdirects, albeit unintentionally, all related thought processes. What we end up with is a plethora of confusion. The fault is not in quantum mechanics but in ourselves, that we are such unrelentingly rational creatures, that so persistently pursue an unsound path that leads to reiterative error.
[2] Because physicists actually care about the real world; mathematicians, not so much.
[3] It must be admitted though that it was not the mathematicians who ever claimed imaginary numbers had anything to do with nature and the real world. Why would they? Reality is not their concern or interest. No, it was physicists themselves who made the mistake. The lesson to be learned by physicists here I expect is to be careful whose petticoat they latch onto. Not all are fabricated substantially enough to sustain their thoughts about reality, though deceptively appearing to do just that for protracted periods of time.
[4] My apologies for not continuing with this here as originally intended. To do so would make this post too long and complicated. Not that transformations among mandalic coordinates are difficult to understand, just that they are very convoluted. This is not a one-point-encodes-one-resident-number plan like that of Descartes we’re talking about here. This is mandala country.
© 2016 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 309-
Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - III

(continued from here)
My objection to the imaginary dimension is not that we cannot see it. Our senses cannot identify probable dimensions either, at least not in the visually compelling manner they can the three Cartesian dimensions. The question here is not whether imaginary numbers are mathematically true. How could they not be? The cards were stacked in their favor. They were defined in such a manner, – consistently and based on axioms long accepted valid, – that they are necessarily mathematically true. There’s a word for that sort of thing. –The word is tautological.– No, the decisive question is whether imaginary numbers apply to the real world; whether they are scientifically true, and whether physicists can truly rely on them to give empirically verifiable results with maps that accurately reproduce mechanisms actually used in nature.[1]
The geometric interpretation of imaginary numbers was established as a belief system using the Cartesian line extending from -1,0,0 through the origin 0,0,0 to 1,0,0 as the sole real axis left standing in the complex plane. In 1843, William Rowan Hamilton introduced two additional axes in a quaternion coordinate system. The new jandk axes, similar to the i axis, encode coordinates of imaginary dimensions. So the complex plane has one real axis, one imaginary; the quaternion system, three imaginary axes, one real, to accomplish which though involved loss of commutative multiplication. The mandalic coordinate system has three real axes upon which are superimposed six probable axes. It is both fully commensurate with the Cartesian system of real numbers and fully commutative for all operations throughout all dimensions as well.[2]
All of these coordinate systems have a central origin point which all other points use as a locus of reference to allow clarity and consistency in determination of location. The mandalic coordinate system is unique in that this point of origin is not a null point of emptiness as in all the other locative systems, but a point of effulgence. In that location where occur Descartes’ triple zero triad (0.0.0) and the complex plane’s real zero plus imaginary zero (ax=0,bi=0), we find eight related hexagrams, all having neutral charge density, each of these consisting of inverse trigrams with corresponding Lines of opposite charge, canceling one another out. These eight hexagrams are the only hexagrams out of sixty-four total possessing both of these characteristics.[3]

So let’s begin now to plot the points of the mandalic coordinate system with the view of comparing its dimensions and points with those of the complex plane.[4] The eight centrally located hexagrams all refer to and are commensurate with the Cartesian triad (0,0,0). In a sense they can be considered eight alternative possible states which can exist in this locale at different times. These are hybrid forms of the four complementary pair of hexagrams found at antipodal vertices of the mandalic cube. The eight vertex hexagrams are those with upper and lower trigrams identical. This can occur nowhere else in the mandalic cube because there are only eight trigrams.[5]

From the origin multiple probability waves of dimension radiate out toward the central points of the faces of the cube, where these divergent force fields rendezvous and interact with reciprocal forces returning from the eight vertices at the periphery. converging toward the origin. Each of these points at the six face centers are common intersections of another eight particulate states or force fields analogous to the origin point except that four originate within this basic mandalic module and four without in an adjacent tangential module. Each of the six face centers then is host to four internal resident hexagrams which share the point in some manner, time-sharing or other. The end result is the same regardless, probabilistic expression of characteristic form and function. There is a possibility that this distribution of points and vectors could be or give rise to a geometric interpretation of the Schrödinger equation, the fundamental equation of physics for describing quantum mechanical behavior. Okay, that’s clearly a wild claim, but in the event you were dozing off you should now be fully awake and paying attention.
The vectors connecting centers of opposite faces of an ordinary cube through the cube center or origin of the Cartesian coordinate system are at 180° to each other forming the three axes of the system corresponding to the number of dimensions. The mandalic cube has 24 such axes, eight of which accompany each Cartesian axis thereby shaping a hybrid 6D/3D coordinate system. Each face center then hosts internally four hexagrams formed by hybridization of trigrams in opposite vertices of diagonals of that cube face, taking one trigram (upper or lower) from one vertex and the other trigram (lower or upper) from the other vertex. This means that a face of the mandalic cube has eight diagonals, all intersecting at the face center, whereas a face of the ordinary cube has only two.[6]

The circle in the center of this figure is intended to indicate that the two pairs of antipodal hexagrams at this central point of the cube face rotate through 90° four times consecutively to complete a 360° revolution. But I am describing the situation here in terms of revolution only to show an analogy to imaginary numbers. The actual mechanisms involved can be better characterized as inversions (reflections through a point), and the bottom line here is that for each diagonal of a square, the corresponding mandalic square has a possibility of 4 diagonals; for each diagonal of a cube, the corresponding mandalic cube has a possibility of 8 diagonals. For computer science, such a multiplicity of possibilities offers a greater number of logic gates in the same computing space and the prospect of achieving quantum computing sooner than would be otherwise likely.[7]
Similarly, the twelve edge centers of the ordinary cube host a single Cartesian point, but the superposed mandalic cube hosts two hexagrams at the same point. These two hexagrams are always inverse hybrids of the two vertex hexagrams of the particular edge. For example, the edge with vertices WIND over WIND and HEAVEN over HEAVEN has as the two hybrid hexagrams at the center point of the edge WIND over HEAVEN and HEAVEN over WIND. Since the two vertices of concern here connect with one another via the horizontal x-dimension, the two hybrids differ from the parents and one another only in Lines 1 and 4 which correspond to this dimension. The other four Lines encode the y- amd z-dimensions, therefore remain unchanged during all transformations undergone in the case illustrated here.[8]

This post began as a description of the structure of the mandalic coordinate system and how it differs from those of the complex plane and quaternions. In the composition, it became also a passable introduction to the method of composite dimension. Additional references to the way composite dimension works can be found scattered throughout this blog and Hexagramium Organum. Basically the resulting construction can be thought of as a tensegrity structure, the integrity of which is maintained by opposing forces in equilibrium throughout, which operate continually and never fail, a feat only nature is capable of. We are though permitted to map the process if we can manage to get past our obsession with and addiction to the imaginary and complex numbers and quaternions.[9]
In our next session we’ll flesh out probable dimension a bit more with some illustrative examples. And possibly try putting some lipstick on that PIG (Presumably Imaginary Garbage) to see if it helps any.
(continuedhere)
Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions (A tesseract). There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons
Notes
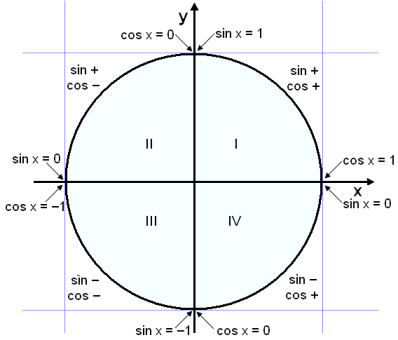
[1] For more on this theme, regarding quaternions, see Footnote [1] here. My own view is that imaginary numbers, complex plane and quaternions are artificial devices, invented by rational man, and not found in nature. Though having limited practical use in representation of rotations in ordinary space they have no legitimate application to quantum spaces, nor do they have any substantive or requisite relation to square root, beyond their fortuitous origin in the Rationalists’ dissection and codification of square root historically, but that part of the saga was thoroughly misguided. We wuz bamboozled. Why persist in this folly? Look carefully without preconception and you’ll see this emperor’s finery is wanting. It is not imperative to use imaginary numbers to represent rotation in a plane. There are other, better ways to achieve the same. One would be to use sin and cos functions of trigonometry which periodically repeat every 360°. (Read more about trigonometric functions here.) Another approach would be to use polar coordinates.
[SOURCE]
A quaternion, on the other hand, is a four-element vector composed of a single real element and three complex elements. It can be used to encode any rotation in a 3D coordinate system. There are other ways to accomplish the same, but the quaternion approach offers some advantages over these. For our purposes here what needs to be understood is that mandalic coordinates encode a hybrid 6D/3D discretized space. Quaternions are applicable only to continuous three-dimensional space. Ultimately, the two reside in different worlds and can’t be validly compared. The important point here is that each has its own appropriate domain of judicious application. Quaternions can be usefully and appropriately applied to rotations in ordinary three-dimensional space, but not to locations or changes of location in quantum space. For description of such discrete spaces, mandalic coordinates are more appropriate, and their mechanism of action isn’t rotation but inversion (reflection through a point.) Only we’re not speaking here about inversion in Euclidean space, which is continuous, but in discrete space, a kind of quasi-Boolean space, a higher-dimensional digital space (grid or lattice space). In the case of an electron this would involve an instantaneous jump from one electron orbital to another.
[2] I think another laudatory feature of mandalic coordinates is the fact that they are based on a thought system that originated in human prehistory, the logic of the primal I Ching. The earliest strata of this monumental work are actually a compendium of combinatorics and a treatise on transformations, unrivaled until modern times, one of the greatest intellectual achievements of humankind of any Age. Yet its true significance is overlooked by most scholars, sinologists among them. One of the very few intellectuals in the West who knew its true worth and spoke openly to the fact, likely at no small risk to his professional standing, was Carl Jung, the great 20th century psychologist and philosopher.
It is of relevance to note here that all the coordinate systems mentioned are, significantly, belief systems of a sort. The mandalic coordinate system goes beyond the others though, in that it is based on a still more extensive thought system, as the primal I Ching encompasses an entire cultural worldview. The question of which, if any, of these coordinate systems actually applies to the natural order is one for science, particularly physics and chemistry, to resolve.
Meanwhile, it should be noted that neither the complex plane nor quaternions refer to any dimensions beyond the ordinary three, at least not in the manner of their current common usage. They are simply alternative ways of viewing and manipulating the two- and three-dimensions described by Euclid and Descartes. In this sense they are little different from polar coordinatesortrigonometry in what they are attempting to depict. Yes, quaternions apply to three dimensions, while polar coordinates and trigonometry deal with only two. But then there is the method of Euler angles which describes orientation of a rigid body in three dimensions and can substitute for quaternions in practical applications.
A mandalic coordinate system, on the other hand, uniquely introduces entirely new features in its composite potential dimensions and probable numbers which I think have not been encountered heretofore. These innovations do in fact bring with them true extra dimensions beyond the customary three and also the novel concept of dimensional amplitudes. Of additional importance is the fact that the mandalic method relates not to rotation of rigid bodies, but to interchangeability and holomalleability of parts by means of inversions through all the dimensions encompassed, a feature likely to make it useful for explorations and descriptions of particle interactions of quantum mechanics. Because the six extra dimensions of mandalic geometry may, in some manner, relate to the six extra dimensions of the 6-dimensional Calabi–Yau manifold, mandalic geometry might equally be of value in string theoryandsuperstring theory.
Itis possible to use mandalic coordinates to describe rotations of rigid bodies in three dimensions, certainly, as inversions can mimic rotations, but this is not their most appropriate usage. It is overkill of a sort. They are capable of so much more and this particular use is a degenerate one in the larger scheme of things.
[3] This can be likened to a quark/gluon soup. It is a unique and very special state of affairs that occurs here. Physicists take note. Don’t let any small-minded pure mathematicians dissuade you from the truth. They will likely write all this off as “sacred geometry.” Which it is, of course, but also much more. Hexagram superpositions and stepwise dimensional transitions of the mandalic coordinate system could hold critical clues to quantum entanglement and quantum gravity. My apologies to those mathematicians able to see beyond the tip of their noses. I was not at all referring to you here.
[4] Hopefully also with dimensions and points of the quaternion coordinate system once I understand the concepts involved better than I do currently. It should meanwhile be underscored that full comprehension of quaternions is not required to be able to identify some of their more glaring inadequacies.
[5] In speaking of "existing at the same locale at different times" I need to remind the reader and myself as well that we are talking here about particles or other subatomic entities that are moving at or near the speed of light,- - -so very fast indeed. If we possessed an instrument that allowed us direct observation of these events, our biologic visual equipment would not permit us to distinguish the various changes taking place. Remember that thirty frames a second of film produces the illusion of motion. Now consider what thirty thousand frames a second of repetitive action would do. I think it would produce the illusion of continuity or standing still with no changes apparent to our antediluvian senses.
[6] Each antipodal pair has four different possible ways of traversing the face center. Similarly, the mandalic cube has thirty-two diagonals because there are eight alternative paths by which an antipodal pair might traverse the cube center. This just begins to hint at the tremendous number of transformational paths the mandalic cube is able to represent, and it also explains why I refer to dimensions involved as potentialorprobable dimensions and planes so formed as probable planes. All of this is related to quantum field theory (QFT), but that is a topic of considerable complexity which we will reserve for another day.
[7] One advantageous way of looking at this is to see that the probabilistic nature of the mandalic coordinate system in a sense exchanges bits for qubits and super-qubits through creation of different levels of logic gates that I have referred to elsewhere as different amplitudes of dimension.
[8] Recall that the Lines of a hexagram are numbered 1 to 6, bottom to top. Lines 1 and 4 correspond to, and together encode, the Cartesian x-dimension. When both are yang (+), application of the method of composite dimension results in the Cartesian value +1; when both yin (-), the Cartesian value -1. When either Line 1 or Line 4 is yang (+) but not both (Boole’s exclusive OR) the result is one of two possible zero formations by destructive interference. Both of these correspond to (and either encodes) the single Cartesian zero (0). Similarly hexagram Lines 2 and 5 correspond to and encode the Cartesian y-dimension; Lines 3 ane 6, the Cartesian z-dimension. This outline includes all 9 dimensions of the hybrid 6D/3D coordinate system: 3 real dimensions and the 6 corresponding probable dimensions. No imaginary dimensions are used; no complex plane; no quaternions. And no rotations. This coordinate system is based entirely on inversion (reflection through a point) and on constructive or destructive interference. Those are the two principal mechanisms of composite dimension.
[9] The process as mapped here is an ideal one. In the real world errors do occur from time to time. Such errors are an essential and necessary aspect of evolutionary process. Without error, no change. And by implication, likely no continuity for long either, due to external damaging and incapacitating factors that a natural world devoid of error never learned to overcome. Errors are the stepping stones of evolution, of both biological and physical varieties.
© 2016 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 308-
Beyond Taoism - Part 1
A Lost Logic of Chinese Antiquity

The 64 Hexagrams of the I Ching
(for interactive version click here)
(continued from here)
In speaking of “Taoist thought” I have often throughout this work used the term as a convenient shorthand for “primeval Chinese thought.” Strictly speaking, this usage is historically incorrect. Laozi is traditionally regarded as the founder of Taoism and is associated with “primordial” or “original” Taoism. Whether he actually existed is disputed. According to tradition the classic text attributed to him, the Tao Te Ching, was written around the 6th century BCE. The oldest extant text, however, dates to the late 4th century BCE. The earliest strata of the I Ching predate both these historical periods by many centuries, if not millennia. Taoism derived its cosmological notions from the philosophy of yin and yang, and from that of the Five Phases or Five Elements. Both these schools of thought were overwhelmingly influenced and shaped by exposure to the oldest known text of ancient Chinese classics, the I Ching.[1]
The actual symbolic logic of Taoism, although derived from the I Ching is extremely simplistic compared with that of the original upon which it is based. Whereas the philosophy of yinandyang as presented in the Tao Te Ching comprises little more than a two-dimensional cycle of two-valued elements, in the I Ching these two represent vectors in a six-dimensional combinatorial manifold of 64 hexagrams (1,2). Clearly, it is a difference like that between night and day. It is, in fact, a literal comparing of 22 with 26, the latter holding many more possibilities. The actual difference[2] in the logic and geometry emerging from the two is greater even than it appears at first. It eventuates not from just a simple geometric progression but from a mandalic intertwining and association of logical elements that give rise to different amplitudes of dimension as well as to a greater number of dimensions. This mandalic interweaving leads also to a richer catalogue of relationship types.[3]
Long viewed as mainly an ancient text of Chinese divination,theI Chingencompasses many more categories of thought - - - among them symbolic logic, geometry, and combinatorics. As a treatise which deals with combinatorics alone, it soars without equal, the first known compendium of combinatorial elements and still one of the finest. The logic and geometry that are embedded in the hexagram system of the I Ching are best understood in terms of dimensions and vectors akin to those in Cartesian systematics, and of logic gates analogous to the truth tables of Boolean algebra. And still the cognoscente will want to explore beyond the pertinency of these disciplines as also beyond Taoism to find the full meaning and intent of the I Ching.[4]
Having existed for millenia, and itself a treatise regarding change[5] in its many aspects, it would be inconceivable that the I Ching as we have it today is as it was in its beginnings. Popular at all societal levels through its entire existence, reinterpretations and reworkings have been myriad. Confucianism in particular interlaced its own brand of philosophical and “ethical-sociopolitical teachings” during and after the fifth century BCE. Other schools of thought added their unique perspectives to what became essentially a massive melting pot of schematization, one not always self-consistent by any means.
When one attempts to uncover the original face of the I Ching the difficulties encountered soon appear insurmountable. If involved in such a venture, it is imperative to bear in mind the bedrock strata of the work were in some ways more ingenuous, and in some more intricate, than the traditional version that has come down to us. The earliest layers arose in context of a preliterate oral tradition with all the many unique aspects of being that entails. In some ways the golden age of the I Ching ended with coming of the written word and literacy. The multidimensional logic that was readily accommodated by an oral tradition foundered and eventually was all but lost in the unrelenting techno-sociological onslaught of script with its associated inevitable linearity. Anyone who hopes to excavate the buried multidimensional logic of the primordial I Ching can expect to do a good deal of laborious digging.
(continuedhere)
Image:Source. Originally from Richard Wilhelm’s and Cary F. Baynes translation “I Ching: Or, Book of Changes” [3rd. ed., Bollingen Series XIX, (Princeton NJ: Princeton University Press, 1967, 1st ed. 1950)]
Notes
[1] Two diagrams known as bagua (or pa kua) that figure prominently in the I Ching and its Commentaries predate their appearances in the I Ching. The Lo Shu Square is sometimes associated with the Later Heaven arrangement of the bagua or trigrams, and the Yellow River Map is sometimes associated with the Earlier Heaven arrangement of trigrams. Both are linked to astronomical events of the sixth millennium BCE. Although part of Chinese mythology, they played an important role in development of Chinese philosophy. The Lo Shu Square is intimately connected with the legacy of the most ancient Chinese mathematical and divinatory traditions. The Lo Shu is the unique normal magic square (1,2) of order three (every normal magic square of order three is derived from Lo Shu by rotation or reflection). [Wikipedia]
[2] Taking into account both changing lines and unchanging lines of hexagrams there are four possible variants for each line: unchanging yin, unchanging yang, changing yin, and changing yang. This results in a total of 46 or 4096 possible different line combinations for each six-line figure. This allows for an enormous number of logical / geometric configurations, all of which map to various points of the mandalic cube or, in terms of Cartesian coordinates, to discretized points of the three-dimensional cube bounded by the eight Cartesian triads which have coordinates of +1 and/or -1 in all possible combinations (corresponding to the eight trigrams.)
To this point changing lines have not been discussed to avoid overcomplicating already complicated matters too soon. Changing lines play an indispensable role in all changes of yin lines to yang lines and vice versa, and therefore, in changes of one hexagram to another. They are also essential elements in formation of the geometric line segment generated by the I Ching hexagrams which I have earlier referred to as the "Taoist line“ and which we have yet to broach fully. Mandalic line segments uniformly comprise sixteen interrelated elements, hexagrams with changing and/or unchanging lines. Though various mandalic line segments have different compositions in terms of six-dimensional hexagrams, these hexagrams can always be reduced in logical and geometrical terms to sixteen bigram forms containing changing and/or unchanging lines. These bigram sets are all identical. No other variants are possible, since 42 equals 16. In this sense there is a single species of mandalic line segment but one which takes on different characteristics in different dimensional contexts. Every hexagram has a commentary appended to each of its six lines, which annotation is intended to be reflected upon only if the line is a changing one at time of consulting the oracle. Justly put, this system is brilliant beyond belief.
[3] Understand here that ‘relationship types’ may variously refer to human relationships in a society, to particle relationships in context of the atom, or to any other species of relationship one might imagine.
[4] For an exhaustive listing of linkstoI Ching related materials on the Web see here.
[5] Indeed, an alternative name of the I Ching in English is Book of Changes. The ensconced multidimensional logic encoded in the original work purports to be a microcosm describing all possible pathways of change, and their incessant changing relationships in the greater macrocosm of the universe.
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 295-
Quantum Naughts and Crosses Revisited - IV
The Cube Sliced and Diced
Cartesian Series: Section FHE


(continued from here)
Below we have the second of three frontal sections through the 3-cube, labeled with the Cartesian coordinates of each point. This “slice” is through a plane that lies between an identity face, which contains the trigram HEAVEN, and an inversion face with the trigram EARTH. As such it does not belong fully to either the one or the other, but it shares some characteristics of both. It is a plane, then, of mediation. Again we see here nine Cartesian ordered triads. Due to an artifact of the “slicing” procedure, the four edge centers deceptively appear as though vertices, and the four face centers could be taken as edge centers. Make note that these appearances are illusory. At the center of this section we have the origin point of the cube, Cartesian (0,0,0).[1]
The key to labeling of points in this section[2] and all those to follow can be found here.
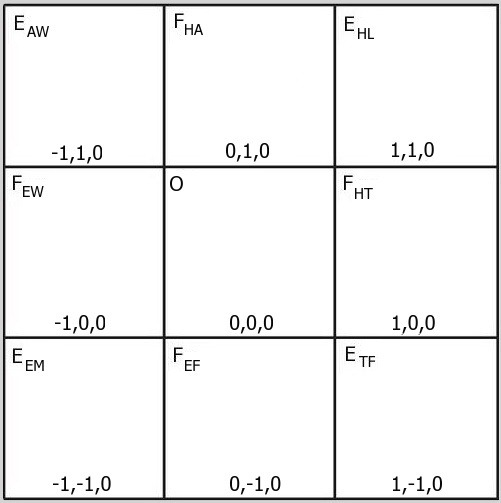
Section FHE
(continuedhere)
Notes
[1] It might be well to note here that the origin point of the coordinate system never appears in either an identity plane or an inversion plane of any of the three section types. All of the planes in which it appears are mediation planes of three dimensions in the case of the Cartesian 3-cube, or of six dimensions in the case of the hybrid mandalic 6D/3D hypercube. This is likely the rationale for why in the I Ching a change involving passage through this central point is referred to as "crossing the Great Water.“ There must be more than coincidence in the fact that Western thought refers to this point as the "origin” and Taoist thought views it as the source and beginning of all things. It’s not that something important was lost in translation. The two notions arose independently, from two very different worldviews. Somehow in the scheme of things, the West came to equate “origin” with "zero" whereas the East came to equate "origin" with “the beginning and end of all things.” Taoism, in particular, sees in this a focus of both creation and dissolution. As we shall soon enough discover, this alternative perspective leads to a different species of arithmetic, one of great antiquity though long lost in the sands of time. Mandalic geometry has unearthed it and will reveal it here, in this blog, for the first time in millennia. As a teaser, it involves a different treatment of what the West calls “zero”. It is an arithmetic more in line with Boolean logic.
[2] The 2-dimensional version of this section is obtained from the x and y coordinates, which by convention are the first and second, respectively, in the Cartesian ordered triads seen here. So the only difference between this section and the FHsectionpreviously viewed is the fact that the z-coordinates here are all zero (0) instead of +1. In our next section, FE, the x and y coordinates will again be as seen here but all z-coordinates will be -1. I believe I detect a trend developing here.
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 289-
Quantum Naughts and Crosses Revisited - III
The Cube Sliced and Diced
Cartesian Series: Section FH


(continued from here)
The first slice through the cube, shown below, the FH section, is the Cartesian xy-plane we’re all familiar with from the 2-dimensional version of the Cartesian coordinate system with the third Cartesian dimension (z) added to the labeling of points. This gives us nine distinct Cartesian triad points: four vertices, four edge centers, and one face center. For all of the points, the third Cartesian dimension (z) is constant in this slice, and the vector value is positive (located toward the viewer with respect to the z=0 value of the z-axis or FHE plane which we’ll be viewing in the next post.)
The key to labeling of points in this section[1] and all those to follow can be found here.
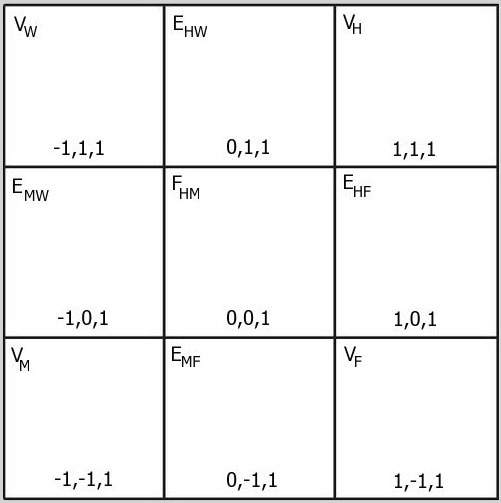
Section FH
(continuedhere)
Notes
[1] This is the frontal section through the cube nearest a viewer. It is Descartes’ xy-plane with label of the third dimension (z) added so each point label shown is a Cartesian ordered triad rather than an ordered pair as textbooks generally show the plane. Why the difference? Because the geometry texts are interested only in demonstrating the two-dimensional plane in isolation, whereas we want to see it as it exists in the context of three or more dimensions. Cartesian triads are shown by convention as (x,y,z), so the xy-plane emerges from the first two coordinates of the points in this section, and all the z-coordinates seen here are positive (+1). The FE plane, which we’ll be viewing in the post after next, has all of its x and y coordinates identical to those seen here but its z-coordinates are all negative (-1).
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 288-
Quantum Naughts and Crosses Revisited - I

(continued from here)
Because nature is ever playful, grokking mandalic geometry is much like a game. We view it as a largely serious one, though, one that involves combinatorics, Boolean logic, and magic squares and cubes. Groundwork for what appears in this post, and several to follow, was laid in May, 2014 in a series titled “Quantum Naughts and Crosses” which began here.
The game is played on a board or field made of three-dimensional coordinates of the Cartesian variety upon which are superimposed the six additional extraordinary dimensions unique to mandalic coordinates. For convenience and ease of representation, the board will be displayed here in two dimensional sections abstracted from the Cartesian cube and from the superimposed mandalic hypercube in a manner analogous to the way computed tomography renders sections of the human body.
The sections commonly used[1] in computed tomographyandmagnetic resonance imaging (MRI) are
- Frontal
- Transverse
- Sagittal
For our purposes here, these can be thought of as
- Planes perpendicular to the z-axis viewed from front to back of cube
- Planes perpendicular to the y-axis viewed from top to bottom of cube
- Planes perpendicular to the x-axis viewed from side right to left of cube
These “cuts” will produce square sections through xy-, xz-, and yz-planes, respectively, of the Cartesian cube and, in the case of the mandalic cube, analogous sections of higher dimension.
These choices of sections are made largely for convenience and ease of communicability. They are mainly of a conventional nature.[2] On the other hand, there is special significance in the fact that all three section types progress from identity faces of the cube, containing the trigram or hexagram HEAVEN, to inversion faces, containing trigram or hexagram EARTH. Some manner of consistency of this sort is necessary. The one chosen here will make things easier as we progress.
Ourgameboard has 27 discretized Cartesian points, centered in 3 amplitude levels about the Cartesian origin (0,0,0).[3] Each point in the figure on the right above is represented by a single small cube, but in the two-dimensional sections we’ll be using for elaboration, they will appear as small squares. So the gameboard is “composed of” 27 cubes arranged in a 3x3x3 pattern. But in descriptions of sections, we will view 9 squares in a 3x3 pattern. This configuration will appear as

But keep in mind each small square in this figure is actually a small cube representing one of the 27 discretized Cartesian points we’ve described.
Until next time, then.
(continuedhere)
Notes
[1] The origin of the word "tomography" is from the Greek word “tomos” meaning “slice” or “section” and “graphe” meaning “drawing.” A CT imaging system produces cross-sectional images or “slices” of anatomy, like the slices in a loaf of bread. The “slices” made are transverse (cross-sections from head to toes or, more often, a portion thereof), but reconstructions of the other types of sections described above are sometimes made, and MRI generates all three types natively.
[2] Admittedly, I’ve chosen the convention here myself and to date it is shared by no one else. Perhaps at some future time it will be a shared convention. One can only hope.
[3] These three discrete amplitude levels of potentiality in the mandalic 9-cube correspond geometrically to face centers, edge centers and vertices of the 3-cube of Cartesian coordinates. They are encoded by the six new potential dimensions interacting with the three ordinary Cartesian dimensions in context of the hybrid 6D/3D mandalic cube. They are a feature of the manner of interaction of all nine temporospatial dimensions acting together in holistic fashion. This should begin to give an idea why there is no Taoist line that can generate a 9-cube in a fashion analogous to the way the Western number line is used to generate the Cartesian / Euclidean 3-cube. The 9-dimensional entity is primeval and a variety of different types of "line" can be derived from it. Similarly, the mandala of the I Ching hexagrams cannot be derived from the logic encoded in any linear structure. An overarching perspective is required to derive first the mandala of hexagrams and then from it, a variety of Taoist line types. Nature may be playful, but it is not nearly as simplistic as our Western science, mathematics, and philosophy would have it.
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 286-
Beyond Descartes - Part 6
The Fiction Formerly Known As the Line


(continued from here)
Rereading the last post a moment ago I see I fell into the same old trap, namely describing a concept arising from an alternative worldview in terms of our Western worldview. It is so astonishingly easy to do this. So it is important always to be on guard against this error of mind.
In saying that the Taoist number line is the basis of its coordinate system I was phrasing the subject in Western terminology, which doesn’t just do an injustice to the truth of the matter, it does violence to it, in the process destroying the reality: that within Taoism, the coordinate system is primary. It precedes the line, which follows from it. What may be the most important difference between the Taoist apprehension of space and that of Descartes lies encoded within that single thought.
Descartes continues the fiction fomented in the Western mind by Euclid that the point and the line have independent reality. Taking that to be true, Descartes constructs his coordinate system using pointsandlines as the elemental building blocks. But to be true to the content and spirit of Taoism, this fabrication must be surrendered. For Taoism, the coordinate system, which models space, or spacetime rather, is primary. Therefore to understand the fictional Taoist line we must begin there, in the holism and the complexity of its coordinate system where dimension, whatever it may be, reigns supreme.[1]
And that means we can no longer disregard composite dimension, postponing discussion of it for a later time, because it is the logical basis on which the I Ching is predicated. It is related to what we today know as combinatorics,Boolean algebra, and probability, and is what gives rise to what I have called the plane of potentiality. It is the very pith of mandalic geometry, what makes it a representation of mandalic spacetime.[2]
(continuedhere)
Notes
[1] In my mind, dimension is a category of physical energetic description before it is a category of geometrical description. When particle physicists speak about “quantum numbers” I think they are actually, whether intended or not, referring to dimensions. If this is true, then our geometries should be constructed to reflect that primordial reality, not arbitrarily as we choose.
[2] In speaking of logic and the I Ching in the same breath I am using the term in its broadest sense as any formal system in which are defined axioms and rules of inference. In reference to the I Ching, the logic involved is far removed from the rationalism bequeathed to Descartes by his times. It is a pre-rationalist logic that prevailed in human history for a very long time before the eventual splitting off of the irrational from the rational. This means also that the I Ching is among other things a viable instrument to access strata of human minds long dormant in historical times, other than possibly, at times, in poetry and art and the work of those select scientists who make extensive use of intuition in the development of their theories.
Note to self: Two contrasting systems of thought based on very different worldviews can never be adequately explained in terms of one another. At times though, for lack of anything better, we necessarily fall back on just such a strategy, however limited, and make the best of it we can.
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 282-
Earlier to Later Heaven: Fugue V Alchemy Is Not a Dirty Word

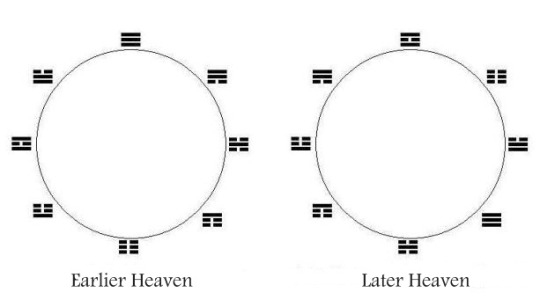
(continued from here)
As is the case with all great mysteries, many different explanations for the origins of both the EARLIER and LATER HEAVEN arrangements of the trigrams have been proposed. In seeking plausible explanations, it is well to keep in mind what the worldview contextual origin of these two different arrangements might have been. The dates of their origins seem to be separated by thousands of years.[1] They grew out of very different worldviews. Still there was a clear attempt to correlate LATER HEAVEN with EARLIER HEAVEN. At the time LATER HEAVEN appeared on the scene, there was a longstanding tradition in place which was not entirely discarded. A kind of conceptual amalgamation took place.[2] The mystery lies in how and why that was accomplished.
Alchemy in its most fundamental aspect has to do with all kinds of relationships and from such a perspective both Earlier Heaven and Later Heaven are alchemical in nature. But differently so. They are reflections of different ways of seeing reality. Both, however, are debilitated, in the sense that they are missing a third dimension. The trigram, having three Lines, is a combination form which maps three dimensions. It cannot be adequately represented by figures of one or two dimensions. Any attempt to do so inevitably provokes injustice to reality by misrepresenting all the combinatoric relationships possible among the eight trigrams.
Placing Earlier Heaven in context of three dimensions enables it to express the full range of relationships and changes that can occur among the eight trigrams, thereby creating a combinatoric system resembling a Boolean lattice. This is very likely the form in which Earlier Heaven was originally understood, whether explicitly or implicitly. At some stage of the development of Chinese philosophy, it lost its clear connection to the third dimension, possibly as a result of the new method of encoding and storing ideas in writing, which demanded linear text, displacing the older oral tradition. And that suggests a possible clue to the mystery of the two trigram arrangements.
(continuedhere)
Notes
[1] Both arrangements of the trigrams are of great antiquity, Earlier Heaven possibly dating to around 3000 BCE and Later Heaven to the 8th century BCE. The point here is that the two arose in widely different cultural contexts having differing worldviews with all that entails. Yet they were related one to the other in the Chinese mind. Imagine, if you will, say, the unlikely amalgamation of the phlogiston theory with the scientific oxygen theory of combustion or with modern thermodynamics in the West. How likely is it that such amalgamations could have occurred though the ideas involved were separated not by millennia but only a few centuries. Something very strange and unexplained happened in the history of Chinese thought when these two widely different arrangements of trigrams were entangled with one another. Things are not as they appear on the surface here. Something hermetic and profound is going on at a deeper level.
[2] Something similar did occur in the West when chemistry took over from alchemy. Though chemistry owes a debt to alchemy for its very existence it is somewhat in denial regarding its origins or at least about this particular aspect of its origins. Having alchemy in its family tree, however, is not something for chemistry to be ashamed about. Alchemy had been practiced in many parts of the world for several millennia before chemistry appeared and can boast many important accomplishments in the history of human cognition. It could be said chemistry threw out the baby with the bath water when it conclusively broke with alchemy, except that it never did do that, not completely. Alchemy in the broadest and best sense has to do with relationships of objects, one to another. Much the same can be said about chemistry.
Modern astronomy also pays homage to an earlier form of ideation when it invokes the notion of a constellation, a term first used in astrology which was considered a scholarly tradition throughout most of its history. Constellations in most cases are composed of stars which, though visible in the same general area, are often located at very different distances from Earth. Nonetheless the tradition of referring to constellations is still in use by astronomers today. Its expediency is considerable as any given point in a celestial coordinate system can easily and unambiguously be assigned to a constellation, 88 of which are officially recognized and used in modern astronomy. The past lives on, in the history of ideas, but changed.
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x + 1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 276-
Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - III
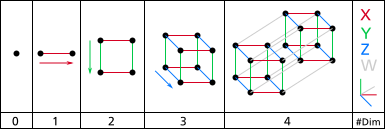
(continued from here)
My objection to the imaginary dimension is not that we cannot see it. Our senses cannot identify probable dimensions either, at least not in the visually compelling manner they can the three Cartesian dimensions. The question here is not whether imaginary numbers are mathematically true. How could they not be? The cards were stacked in their favor. They were defined in such a manner, – consistently and based on axioms long accepted valid, – that they are necessarily mathematically true. There’s a word for that sort of thing. –The word is tautological.– No, the decisive question is whether imaginary numbers apply to the real world; whether they are scientifically true, and whether physicists can truly rely on them to give empirically verifiable results with maps that accurately reproduce mechanisms actually used in nature.[1]
The geometric interpretation of imaginary numbers was established as a belief system using the Cartesian line extending from -1,0,0 through the origin 0,0,0 to 1,0,0 as the sole real axis left standing in the complex plane. In 1843, William Rowan Hamilton introduced two additional axes in a quaternion coordinate system. The new jandk axes, similar to the i axis, encode coordinates of imaginary dimensions. So the complex plane has one real axis, one imaginary; the quaternion system, three imaginary axes, one real, to accomplish which though involved loss of commutative multiplication. The mandalic coordinate system has three real axes upon which are superimposed six probable axes. It is both fully commensurate with the Cartesian system of real numbers and fully commutative for all operations throughout all dimensions as well.[2]
All of these coordinate systems have a central origin point which all other points use as a locus of reference to allow clarity and consistency in determination of location. The mandalic coordinate system is unique in that this point of origin is not a null point of emptiness as in all the other locative systems, but a point of effulgence. In that location where occur Descartes’ triple zero triad (0.0.0) and the complex plane’s real zero plus imaginary zero (ax=0,bi=0), we find eight related hexagrams, all having neutral charge density, each of these consisting of inverse trigrams with corresponding Lines of opposite charge, canceling one another out. These eight hexagrams are the only hexagrams out of sixty-four total possessing both of these characteristics.[3]

So let’s begin now to plot the points of the mandalic coordinate system with the view of comparing its dimensions and points with those of the complex plane.[4] The eight centrally located hexagrams all refer to and are commensurate with the Cartesian triad (0,0,0). In a sense they can be considered eight alternative possible states which can exist in this locale at different times. These are hybrid forms of the four complementary pair of hexagrams found at antipodal vertices of the mandalic cube. The eight vertex hexagrams are those with upper and lower trigrams identical. This can occur nowhere else in the mandalic cube because there are only eight trigrams.[5]

From the origin multiple probability waves of dimension radiate out toward the central points of the faces of the cube, where these divergent force fields rendezvous and interact with reciprocal forces returning from the eight vertices at the periphery. converging toward the origin. Each of these points at the six face centers are common intersections of another eight particulate states or force fields analogous to the origin point except that four originate within this basic mandalic module and four without in an adjacent tangential module. Each of the six face centers then is host to four internal resident hexagrams which share the point in some manner, time-sharing or other. The end result is the same regardless, probabilistic expression of characteristic form and function. There is a possibility that this distribution of points and vectors could be or give rise to a geometric interpretation of the Schrödinger equation, the fundamental equation of physics for describing quantum mechanical behavior. Okay, that’s clearly a wild claim, but in the event you were dozing off you should now be fully awake and paying attention.
The vectors connecting centers of opposite faces of an ordinary cube through the cube center or origin of the Cartesian coordinate system are at 180° to each other forming the three axes of the system corresponding to the number of dimensions. The mandalic cube has 24 such axes, eight of which accompany each Cartesian axis thereby shaping a hybrid 6D/3D coordinate system. Each face center then hosts internally four hexagrams formed by hybridization of trigrams in opposite vertices of diagonals of that cube face, taking one trigram (upper or lower) from one vertex and the other trigram (lower or upper) from the other vertex. This means that a face of the mandalic cube has eight diagonals, all intersecting at the face center, whereas a face of the ordinary cube has only two.[6]
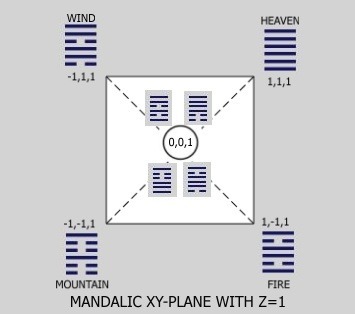
The circle in the center of this figure is intended to indicate that the two pairs of antipodal hexagrams at this central point of the cube face rotate through 90° four times consecutively to complete a 360° revolution. But I am describing the situation here in terms of revolution only to show an analogy to imaginary numbers. The actual mechanisms involved can be better characterized as inversions (reflections through a point), and the bottom line here is that for each diagonal of a square, the corresponding mandalic square has a possibility of 4 diagonals; for each diagonal of a cube, the corresponding mandalic cube has a possibility of 8 diagonals. For computer science, such a multiplicity of possibilities offers a greater number of logic gates in the same computing space and the prospect of achieving quantum computing sooner than would be otherwise likely.[7]
Similarly, the twelve edge centers of the ordinary cube host a single Cartesian point, but the superposed mandalic cube hosts two hexagrams at the same point. These two hexagrams are always inverse hybrids of the two vertex hexagrams of the particular edge. For example, the edge with vertices WIND over WIND and HEAVEN over HEAVEN has as the two hybrid hexagrams at the center point of the edge WIND over HEAVEN and HEAVEN over WIND. Since the two vertices of concern here connect with one another via the horizontal x-dimension, the two hybrids differ from the parents and one another only in Lines 1 and 4 which correspond to this dimension. The other four Lines encode the y- amd z-dimensions, therefore remain unchanged during all transformations undergone in the case illustrated here.[8]

This post began as a description of the structure of the mandalic coordinate system and how it differs from those of the complex plane and quaternions. In the composition, it became also a passable introduction to the method of composite dimension. Additional references to the way composite dimension works can be found scattered throughout this blog and Hexagramium Organum. Basically the resulting construction can be thought of as a tensegrity structure, the integrity of which is maintained by opposing forces in equilibrium throughout, which operate continually and never fail, a feat only nature is capable of. We are though permitted to map the process if we can manage to get past our obsession with and addiction to the imaginary and complex numbers and quaternions.[9]
In our next session we’ll flesh out probable dimension a bit more with some illustrative examples. And possibly try putting some lipstick on that PIG (Presumably Imaginary Garbage) to see if it helps any.
(continuedhere)
Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions (A tesseract). There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons
Notes
[1] For more on this theme, regarding quaternions, see Footnote [1] here. My own view is that imaginary numbers, complex plane and quaternions are artificial devices, invented by rational man, and not found in nature. Though having limited practical use in representation of rotations in ordinary space they have no legitimate application to quantum spaces, nor do they have any substantive or requisite relation to square root, beyond their fortuitous origin in the Rationalists’ dissection and codification of square root historically, but that part of the saga was thoroughly misguided. We wuz bamboozled. Why persist in this folly? Look carefully without preconception and you’ll see this emperor’s finery is wanting. It is not imperative to use imaginary numbers to represent rotation in a plane. There are other, better ways to achieve the same. One would be to use sin and cos functions of trigonometry which periodically repeat every 360°. (Read more about trigonometric functions here.) Another approach would be to use polar coordinates.

[SOURCE]
A quaternion, on the other hand, is a four-element vector composed of a single real element and three complex elements. It can be used to encode any rotation in a 3D coordinate system. There are other ways to accomplish the same, but the quaternion approach offers some advantages over these. For our purposes here what needs to be understood is that mandalic coordinates encode a hybrid 6D/3D discretized space. Quaternions are applicable only to continuous three-dimensional space. Ultimately, the two reside in different worlds and can’t be validly compared. The important point here is that each has its own appropriate domain of judicious application. Quaternions can be usefully and appropriately applied to rotations in ordinary three-dimensional space, but not to locations or changes of location in quantum space. For description of such discrete spaces, mandalic coordinates are more appropriate, and their mechanism of action isn’t rotation but inversion (reflection through a point.) Only we’re not speaking here about inversion in Euclidean space, which is continuous, but in discrete space, a kind of quasi-Boolean space, a higher-dimensional digital space (grid or lattice space). In the case of an electron this would involve an instantaneous jump from one electron orbital to another.
[2] I think another laudatory feature of mandalic coordinates is the fact that they are based on a thought system that originated in human prehistory, the logic of the primal I Ching. The earliest strata of this monumental work are actually a compendium of combinatorics and a treatise on transformations, unrivaled until modern times, one of the greatest intellectual achievements of humankind of any Age. Yet its true significance is overlooked by most scholars, sinologists among them. One of the very few intellectuals in the West who knew its true worth and spoke openly to the fact, likely at no small risk to his professional standing, was Carl Jung, the great 20th century psychologist and philosopher.
It is of relevance to note here that all the coordinate systems mentioned are, significantly, belief systems of a sort. The mandalic coordinate system goes beyond the others though, in that it is based on a still more extensive thought system, as the primal I Ching encompasses an entire cultural worldview. The question of which, if any, of these coordinate systems actually applies to the natural order is one for science, particularly physics and chemistry, to resolve.
Meanwhile, it should be noted that neither the complex plane nor quaternions refer to any dimensions beyond the ordinary three, at least not in the manner of their current common usage. They are simply alternative ways of viewing and manipulating the two- and three-dimensions described by Euclid and Descartes. In this sense they are little different from polar coordinatesortrigonometry in what they are attempting to depict. Yes, quaternions apply to three dimensions, while polar coordinates and trigonometry deal with only two. But then there is the method of Euler angles which describes orientation of a rigid body in three dimensions and can substitute for quaternions in practical applications.
A mandalic coordinate system, on the other hand, uniquely introduces entirely new features in its composite potential dimensions and probable numbers which I think have not been encountered heretofore. These innovations do in fact bring with them true extra dimensions beyond the customary three and also the novel concept of dimensional amplitudes. Of additional importance is the fact that the mandalic method relates not to rotation of rigid bodies, but to interchangeability and holomalleability of parts by means of inversions through all the dimensions encompassed, a feature likely to make it useful for explorations and descriptions of particle interactions of quantum mechanics. Because the six extra dimensions of mandalic geometry may, in some manner, relate to the six extra dimensions of the 6-dimensional Calabi–Yau manifold, mandalic geometry might equally be of value in string theoryandsuperstring theory.
Itis possible to use mandalic coordinates to describe rotations of rigid bodies in three dimensions, certainly, as inversions can mimic rotations, but this is not their most appropriate usage. It is overkill of a sort. They are capable of so much more and this particular use is a degenerate one in the larger scheme of things.
[3] This can be likened to a quark/gluon soup. It is a unique and very special state of affairs that occurs here. Physicists take note. Don’t let any small-minded pure mathematicians dissuade you from the truth. They will likely write all this off as “sacred geometry.” Which it is, of course, but also much more. Hexagram superpositions and stepwise dimensional transitions of the mandalic coordinate system could hold critical clues to quantum entanglement and quantum gravity. My apologies to those mathematicians able to see beyond the tip of their noses. I was not at all referring to you here.
[4] Hopefully also with dimensions and points of the quaternion coordinate system once I understand the concepts involved better than I do currently. It should meanwhile be underscored that full comprehension of quaternions is not required to be able to identify some of their more glaring inadequacies.
[5] In speaking of "existing at the same locale at different times" I need to remind the reader and myself as well that we are talking here about particles or other subatomic entities that are moving at or near the speed of light,- - -so very fast indeed. If we possessed an instrument that allowed us direct observation of these events, our biologic visual equipment would not permit us to distinguish the various changes taking place. Remember that thirty frames a second of film produces the illusion of motion. Now consider what thirty thousand frames a second of repetitive action would do. I think it would produce the illusion of continuity or standing still with no changes apparent to our antediluvian senses.
[6] Each antipodal pair has four different possible ways of traversing the face center. Similarly, the mandalic cube has thirty-two diagonals because there are eight alternative paths by which an antipodal pair might traverse the cube center. This just begins to hint at the tremendous number of transformational paths the mandalic cube is able to represent, and it also explains why I refer to dimensions involved as potentialorprobable dimensions and planes so formed as probable planes. All of this is related to quantum field theory (QFT), but that is a topic of considerable complexity which we will reserve for another day.
[7] One advantageous way of looking at this is to see that the probabilistic nature of the mandalic coordinate system in a sense exchanges bits for qubits and super-qubits through creation of different levels of logic gates that I have referred to elsewhere as different amplitudes of dimension.
[8] Recall that the Lines of a hexagram are numbered 1 to 6, bottom to top. Lines 1 and 4 correspond to, and together encode, the Cartesian x-dimension. When both are yang (+), application of the method of composite dimension results in the Cartesian value +1; when both yin (-), the Cartesian value -1. When either Line 1 or Line 4 is yang (+) but not both (Boole’s exclusive OR) the result is one of two possible zero formations by destructive interference. Both of these correspond to (and either encodes) the single Cartesian zero (0). Similarly hexagram Lines 2 and 5 correspond to and encode the Cartesian y-dimension; Lines 3 ane 6, the Cartesian z-dimension. This outline includes all 9 dimensions of the hybrid 6D/3D coordinate system: 3 real dimensions and the 6 corresponding probable dimensions. No imaginary dimensions are used; no complex plane; no quaternions. And no rotations. This coordinate system is based entirely on inversion (reflection through a point) and on constructive or destructive interference. Those are the two principal mechanisms of composite dimension.
[9] The process as mapped here is an ideal one. In the real world errors do occur from time to time. Such errors are an essential and necessary aspect of evolutionary process. Without error, no change. And by implication, likely no continuity for long either, due to external damaging and incapacitating factors that a natural world devoid of error never learned to overcome. Errors are the stepping stones of evolution, of both biological and physical varieties.
© 2016 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 308-
Beyond Taoism - Part 5
A Vector-based Probabilistic
Number System
Part II

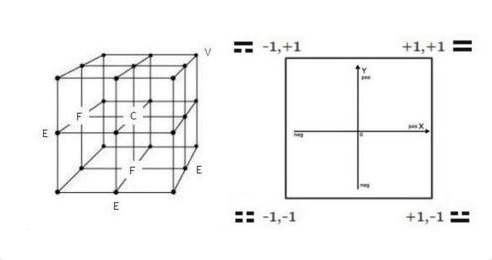
(continued from here)
Taoism and the primordial I Chingare in agreement that temporal changes have two different aspects: sequent and cyclic. Western thought in general follows suit. The I Ching differs from the other two in asserting that the direction of change - for both sequent and cyclic change - is fully reversible, with the proviso that sufficiently small units of measurement are involved.[1] The probability that reversal can be achieved diminishes proportionately to the magnitude of change that has taken place.[2]
Taoist appropriation of bigrams and trigrams of the I Ching to model such phenomena as change of seasons and phases of the moon is plausible if not quite legitimate. The natural phenomena so modeled are macroscopic and vary continuouslyandinexorably throughout an ever-repeating cyclic spectrum. And there’s the rub.
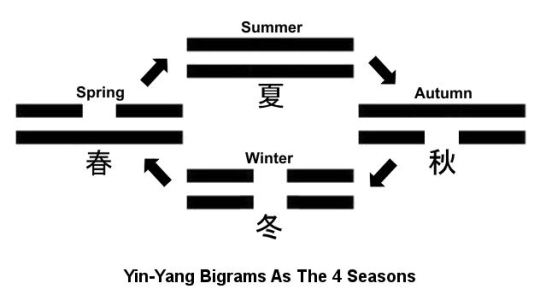
As they occur and function in the I Ching bigrams and trigrams are dicontinuous discrete elements, formed by other similarly discontinuous discretized entities, and they follow evolutionary courses which are most often nonrepetitive. So the Taoist usage is misleading at best, annihilative at worst. Unfortunately, as the I Ching itself evolved through centuries of commentaries and reinterpretations, it became ever more contaminated and tainted by these Taoist corruptions of meaning, at the same time that it was being inundated by Confucian sociological and ethical reworkings. What we have today is an amalgam, the various parts of which do not sit well with one another.[3]
Though it may in part be hyperbole to prove a point, the stark difference between the two approaches, that of Taoism and that of the I Ching, is epitomized by comparison of the Taoist diagram of the cycle of seasons with diagrams at the top and bottom of the page, which are based on the number, logic, and coordinate systems of The Book of Changes.[4] The increased complexity of the latter diagrams should not prove a stumbling block, as they can be readily understood in time with focus and attention to detail. The important take-away for now is that in the I Ching bigrams exist within a larger dimensional context than the Taoist diagram avows, and this context makes all their interactions more variable, conditional, and complex. As well, the same can be said of trigrams and hexagrams.
One of the more important aspects of these differences has to do with the notion of equipotentiality. As bigrams and trigrams function within higher dimensional contexts in the I Ching, this introduces a possibility of multiple alternative paths of movement and directions of change. Put another way, primordial I Ching logic encompasses many more degrees of freedom than does the logic of Taoism.[5] There is no one direction or path invariably decreed or favored. An all-important element of conditionality prevails. And that might be the origin of what quantum mechanics has interpreted as indeterminism or chance.
Next up, a closer look at equipotentiality and its further implications.

Section FH(n)[6]
(continuedhere)
Notes
[1] There are exceptions. Taoist alchemy describes existence of certain changes that admit reversibility under special circumstances. Other than the Second Law of Thermodynamics (which is macroscopic in origin, not result of any internally irreversible microscopic properties of the bodies), the laws of physics neglect all distinction between forward-moving timeandbackward-moving time. Chemistry recognizes existence of certain states of equilibrium in which the rates of change in both directions are equal. Other exceptions likely occur as well.
[2] Since change is quantized in the I Ching, which is to say, it is divided into small discretized units, which Line changes model, the magnitude of change is determined by the number of Line changes that have occurred between Point A and Point B in spacetime. Reversal is far easier to achieve if only a single Line change has occurred than if three or four Lines have changed for example.
[3] Ironically, Taoism itself has pointed out the perils of popularity. Had the I Ching been less popular, less appealing to members of all strata of society, it would have traveled through time more intact. Unless, of course, it ended up buried or burned. What is fortunate here is that much of the primordial logic of the I Ching can be reconstructed by focusing our attention on the diagrammatic figures and ignoring most of the attached commentary.
[4] These diagrams do not occur explicitly in the I Ching. The logic they are based on, though, is fully present implicitly in the diagramatic structural forms of hexagrams, trigrams, and bigrams and the manner of their usage in I Ching divinatory practices.
[5] Or, for that matter, than does the logic of Cartesian coordinate space if we take into account the degrees of freedom of six dimensional hexagrams mapped by composite dimensional methodology to model mandalic space. (See Note [4] here for important related remarks.)
[6] This is the closest frontal section to the viewer through the 3-dimensional cube using Taoist notation. See here for further explanation. Keep in mind this graph barely hints at the complexity of relationships found in the 6-dimensional hypercube which has in total 4096 distinct changing and unchanging hexagrams in contrast to the 16 changing and unchanging trigrams we see here. Though this model may be simple by comparison, it will nevertheless serve us well as a key to deciphering the number system on which I Ching logic is based as well as the structure and context of the geometric line that can be derived by application of reductionist thought to the associated mandalic coordinate system of the I Ching hexagrams. We will refer back to this figure for that purpose in the near future.
© 2016 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 300-
Beyond Taoism - Part 4
A Vector-based Probabilistic
Number System
Introduction


(continued from here)
Leibniz erred in concluding the hexagrams of the I Ching were based on a number system related to his own binary number system. He had a brilliant mind but was just as fallible as the rest of us. He interpreted the I Ching in terms of his own thought forms, and he saw the hexagrams as a foreshadowing of his own binary arithmetic.[1]
So in considering the hexagram Receptive, Leibniz understood the number 0; in the hexagram Return, the number 1; in the hexagram Army, the number 2; in the hexagram Approach, the number 3; in the hexagram Modesty, the number 4; in the hexagram Darkening of the Light, the number 5; and so on, up to the hexagram Creative, in which he saw the number 63.[2] His error is perhaps excusable in light of the fact that the Taoists, though much closer to the origin of the I Ching in time, themselves misinterpreted the number system it was based on.[3]

From our Western perspectiveI Ching hexagrams are composed of trigrams, tetragrams, bigrams, and ultimately yinandyang Lines. From the native perspective of the I Ching this order of arrangement is putting the cart before the horse. Dimensions and their interactions are, in the view of I Ching philosophy and mandalic geometry, antecedent logically and materially to any cognitive parts we may abstract from them. Taoism in certain contexts has abstracted the parts and caused them to appear as if primary. It has the right to do so if creating its own philosophy, but not as interpretation of the logic of the I Ching. It is a fallacy if so intended.[4]
The Taoists borrowed from the I Ching two-dimensional numbers, treated them as one-dimensional and based their quasi-modular number system on the dimension-deficient result. This is the way they arrived at their seasonal cycle consisting of bigrams: old yin (Winter), young yang (Spring), old yang (Summer), young yin (Autumn), old yin (Winter), and so forth. This represents a very much impoverished and impaired version of the original configuration in the primal strata of the I Ching.[5]

The number system of the I Ching is not a linear one-dimensional number system like the positional decimal number system of the West; nor is it like the positional binary number system invented by Leibniz. It is not even like the quasi-modular number system of Taoism. The key to the number system of the hexagrams is located not in the 64 unchanging explicit hexagrams, but rather in the changing implicit hexagrams found only in the divination practice associated with the I Ching. These number 4032.[6] The manner in which these operate, however, is actually fairly simple and is uniform throughout the system. So once understood, they can be safely relegated to the implicit background, coming into play only during procedures involving divination or in attempts to understand the system fully, logically and materially. When dealing with more ordinary circumstances just the 64 more stable hexagrams need be attended to in a direct and explicit manner.
The Taoist sequence of bigrams is in fact a corruption of the far richer asequential multidimensional arrangement of bigrams that occurs in I Ching hexagrams and divination. There we see that change can occur from any one of the four stable bigrams to any other. If this is so then no single sequence can do justice to the total number possible. The ordering of bigrams presented by Taoism is just one of many that make up the real worlds of nature and humankind. Taoism imparts special significance to this sequence; the primal I Ching does not. It views all possible pathways of change as equally likely.[7]
Next time around we will look further into the implications of this equipotentiality and see how it plays out in regard to the number system of the I Ching.

Section FH(n)[8]
(continuedhere)
Notes
[1] By equating yang with 1 and yin with 0 it is possibletosequence the 64 I Ching hexagrams according to binary numbers 0 through 63. The mere fact that this is possible does not, however, mean that this was intended at the time the hexagrams were originally formulated. Unfortunately, this arrangement of hexagrams seems to have been the only one of which Leibniz had knowledge. This sequence was, in fact, the creation of the Chinese philosopher Shao Yong (1011–1077). It did not exist in human mentation prior to the 11th century CE.
This arrangement was set down by the Song dynasty philosopher Shao Yong (1011–1077 CE), six
centuries before Wilhelm Leibniz described binary notation. Leibniz published ‘De progressione
dyadica’ in 1679. In 1701 the Jesuit Joachim Bouvet wrote to him enclosing a copy of Shao Yong’s 'Xiantian cixu’ (Before Heaven sequence). [Source]
Note also that the author of Calling crane in the shade, the source quoted above, calls attention to confusion that exists about whether the “true binary sequence of hexagrams” should begin with the lowest line as the least significant bit (LSB) or the highest line. He points out that the Fuxi sequence as transmitted by Shao Yong in both circular and square diagrams takes the highest line as the LSB, although in fact it would make more sense in consideration of how the hexagram form is interpreted to take the lowest line as the LSB. My thinking is that either Shao Yong misinterpreted the usage of hexagram form or, more likely, the conventional interpretation of the Shao Yong diagrams is incorrect. Here I have chosen to use the lowest line of the hexagram as the LSB, and I think it possible Leibniz may have done the same.
If one considers the circular Shao Yong diagram, the easier of the two to follow, one can reconstruct the binary sequence, with the lowest line as LSB, by beginning with the hexagram EARTH at the center lower right half of the circle, reading all hexagrams from outside line (bottom) to inside line (top), progressing counterclockwise to MOUNTAIN over WIND at top center, then jumping to hexagram MOUNTAIN over EARTH bottom center of left half of the circle, and progressing clockwise to hexagram HEAVEN at top center. Of the two, this is the interpretation that makes the more sense to me and the one I have followed here, despite the fact that it is not the received traditional interpretation of the Shao Yong sequence. Historical transmissions have not infrequently erred. Admittedly it is difficult to decipher all Lines of some of the hexagrams in the copy Leibniz received due to passage of time and its effects on paper and ink. Time is not kind to ink and paper, nor for that matter to flesh and products of intellect.
In the final analysis, which of the two described interpretations is the better is moot because neither conforms to the logic of the I Ching which is not binary to begin with. Moreover, there is a third interpretation of the Shao Yong sequence that is superior to either described here. It is not binary-based. And why should it be? After all the Fuxi trigram sequence which Shao Yong took as model for his hexagram sequence is itself not binary-based. Perhaps we’ll consider that interpretation somewhere down the road. For now, the main take-away is that Leibniz, in his biased interpretation of the I Ching hexagrams made one huge mistake. Ironically, had he not some 22 years prior already invented binary arithmetic, this error likely would have led him to invent it. It was “in the cards” as they say. At least in certain probable worlds.
[2]ReceptiveandCreative are alternative names for the hexagrams EarthandHeaven, respectively. The sequence detailed can be continued ad infinitum using yin-yang notation, though of course this takes us beyond the realm of hexagrams into what would be, for mandalic geometry and logistics of the I Ching, domains of dimensions numbering more than six. Keep in mind here though that Leibniz was not thinking in terms of dimension but an alternative method of expressing the prevalent base 10 positional number system notation of the West. He held in his grasp the key to unlocking an even greater treasure but apparently never once saw that was so. This seems strange considering his broadly diversified interests and pursuits in the fields of mathematics, physics, symbolic logic, information science, combinatorics, and in the nature of space. Moreover, his concern with these was not just as separate subjects of investigation. He envisaged uniting all of them in a universal language capable of expressing mathematical, scientific, and metaphysical concepts.
[3] Earlier in this blog I have too often confused Taoism with pre-Taoism. The earliest strata of the I Ching belong to an age that preceded Taoism by centuries, if not millennia. Though Taoism was largely based on the philosophy and logic of the I Ching, it didn’t always interpret source materials correctly, or possibly at times it intentionally used source materials in new ways largely foreign to the originals. The number system of the I Ching is a case in point.
In the interest of full disclosure, I am not an expert in the history or philosophy of Taoism. Taoist philosophies are diverse and extensive. No one has a complete set or grasp of all the thoughts, practices and techniques of Taoism. The two core Taoist texts, the Tao Te ChingandChuang-tzu, provide the philosophical basis of Taoism which derives from the eight trigrams (bagua) of Fu Xi, c. 2700 BCE, the various combinations of which created the 64 hexagrams documented in the I Ching. The Daozang, also referred to as the Taoist canon, consists of around 1,400 texts that were collected c. 400, long after the two classic texts mentioned. What I describe as Taoist thought then is abstracted in some manner from a huge compilation, parts of which may well differ from what is presented here. Similar effects of time and history can be discerned in Buddhism, Christianity, Islam and secular schools of thought like Platonism,Aristotelianism,Humanism, etc.
[4] Recent advances in the sciences have begun to raise new ideas regarding the structure of reality. Many of these have parallels in Eastern thought. There has been a shift away from the reductionist view in which things are explained by breaking them down then looking at their component parts, towards a more holistic view. Quantum physics notably has changed the way reality is viewed. There are no certainties at a quantum level, and the experimenter is necessarily part of the experiment. In this new view of nature everything is linked and man is himself one of the linkages.
[5] It is not so much that this is incorrect as that it isextremelylimiting with respect to the capacities of the I Ching hexagrams. A special case has here been turned into a generalization that purports to cover all bases. This may serve well enough within the confines of Taoism but it comes nowhere near elaborating the number system native to the I Ching. We would be generous in describing it as a watered down version of a far more complex whole. Through the centuries both Confucianism and Taoism restructured the I Ching to make it conducive to their own purposes. They edited it and revised it repeatedly, generating commentary after commentary, which were admixed with the original, so that the I Ching as we have it today, the I Ching of tradition, is a hodgepodge of many convictions and many opinions. This makes the quest for the original features of the I Ching somewhat akin to an archaeological dig. I find it not all that surprising that the oracular methodology of consulting the I Ching holds possibly greater promise in this endeavor than the written text. The early oral traditions were preserved better, I think, by the uneducated masses who used the I Ching as their tool for divination than by philosophers and scholars who, in their writings, played too often a game of one-upmanship with the original.
[6] A Line can be either yin or yang, changing or unchanging. Then there are four possible Line types and six Lines to a hexagram. This gives a total of 4096 changing and unchanging hexagrams (46 = 4096). Since there are 64 unchanging hexagrams (26 = 64) there must be 4032 changing hexagrams (4096-64 = 4032).
[7] This calls to mind the path integral formulation of quantum mechanics which was developed in its complete form by Richard Feynman in 1948. See, for example, this description of the path integral formulation in context of the double-slit experiment, the quintessential experiment of quantum mechanics.
[8] This is the closest frontal section to the viewer through the 3-dimensional cube using Taoist notation. See here for further explanation. Keep in mind this graph barely hints at the complexity of relationships found in the 6-dimensional hypercube which has in total 4096 distinct changing and unchanging hexagrams in contrast to the 16 changing and unchanging trigrams we see here. Though this model may be simple by comparison, it will nevertheless serve us well as a key to deciphering the number system on which I Ching logic is based as well as the structure and context of the geometric line that can be derived by application of reductionist thought to the associated mandalic coordinate system of the I Ching hexagrams. We will refer back to this figure for that purpose in the near future.
© 2016 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 299-
I have misguided all of you. The number of blends you can produce using the method I described in the last post is not N!; that’s the number of blends you can produce if you use every object in the set. The real number is much, much larger, and looks like this:

The number of ways you can take k objects from a set with N objects in it and order those combinations is equal to N!/(N-k)!, or the expression inside the big parentheses above. The weird shit on the left just says take that expression for every value of k from 1 to N and add the results all together. This is A Big Number. According to this helpful website, that number for 7 (like in mint plus sage) is 13,699. Compare 7!’s value of 5,040- more than double. 13! was equal to 6,227,020,800; the value of this function for N = 13 is 16,927,797,485. If I thought this method was a terrible way to make blends because it produced too many before, it’s much worse in reality.
Another of the of the ways in which ‘blends as permutations’ (well, k-permutations) model sucks is that there’s no guarantee that any given 'possible blend’ will contain material from both words. From mintand sage, both mintand sage are considered possible blends in this model! It’s a pretty solid generalization about blends that they contain elements from both words. How do we capture this in our model?
Well, let’s say that, instead of one bag, you have two- one for each word- and every time you have to draw a letter, you flip a coin. Heads means you draw from word A, tails means you draw from word B. You can only stop once you’ve drawn at least one sound from both bags (although you need not stop then), and for convenience’s sake let’s just say that once you’ve emptied one bag you stop flipping the coin and just draw from the other one. (An unintended consequence of introducing the flipping coin is that most of the time, the blends produced this way will contain roughly equal amounts of sounds from words A and B, but let’s ignore this for a second and just say that all possible blends are equally likely.)
How many blends can you produce in this way? Given what we learned above, this is pretty simple.

Scrapping the requirement that sounds from both words must end up in the blend, what about what sounds begin a blend? Seems like most blends start with a sound that starts one of the donor words, so let’s constrain the output to blends starting with a1 or b1. How many blends can we make in this way?
Well, let’s start with the set {1, 2, 3, 4, 5, 6, 7}, and say that the k-permutations all have to start with 7. There’s one permutation for k = 1 that fits this criterion- 7. After that, it’s 7 followed by every k-permutation of the set containing all the same members, except 7, as the set before- that is, every k-permutation of the set {1, 2, 3, 4, 5, 6}. So 1, for 7, plus every k-permutation of a set with 7-1 members.

So, if two members, a1 and b1, of a set of size N can start the k-permutations, the number is just double the above.
Let’s say you want to combine this requirement with the one above that both words must contribute to the blend!

This is getting ugly fast.
So here’s the golden question: Why am I counting all of these possible blends? Who on Earth cares how many of them exist? Here’s where I lay out my evil research plan:
I’m going to ask research subjects to form blends from various pairs of words, then compare the set of blends they collectively produce to the set of all possible blends under each of these models. And if models with certain constraints on them overgenerate less than the worst imaginable case to a statistically significant degree, we will have rigorously shown that those constraints meaningfully capture something about blend-formation in English.
Yeah, beat that!
So what, exactly, is a blend? How do you make one? What kinds of blends are permissible? And… drumroll please… how can we categorize this in a mathematical way?
[cymbal clash]
Okay, maybe that question doesn’t excite anyone else but me. If you’re not super jazzed about that as a problem to be solved, well, sucks for both of us, I’m thinking it’s going to be pretty important to my research. More importantly in the short term, this blog post might be even more unreadable than the ones about academic sources. But if that question does tickle your brain cells, even a little bit, do read on- I’ll try to keep it fun.
One hypothetical way to make a blend of two words, let’s say mintand sage, is to write all the sounds in both words on little pieces of paper, put the pieces of paper in a hat, and pull as many as you like (or until you run out). There are very few rules to this game, and you can probably figure them out yourself, but I’ll say them just to be complete.
- You wrote each word (in a phonemic transcription) in big symbols on a piece of paper and tore each sound out individually. You didn’t put any other sounds in the hat. That means that, because mintand sage don’t repeat any sounds, you can only use each sound once. (If you wanted to blend lettuceand lemon, you could use /l/, /ɛ/, and /ə/ twice each, since there are two of each between lettuceand lemon: /‘lɛ.təs/, /'lɛ.mən/.)
- More subtly, you didn’t tear any of the sounds in two- you’re stuck with how you chopped up the words when you started writing. You may be thinking, 'Why would that matter? What would you even do with half of an /m/?’ You’re right, that wouldn’t make much sense, but consider sage /sedʒ/: that last sound, the J-sound, is sort of one sound and sort of two. Phonetically, that is in physical reality, it’s a [d] followed very quickly by a [ʒ] (the middle sound in vision). The International Phonetic Alphabet reflects this phonetic reality by telling us to write [dʒ] with two letters, even though a ligature- a combination of the two letters- exists, and looks like this: <ʤ> But most linguists believe that, in the mind and in the language, the [d] and the [ʒ] together form a unit /dʒ/ that can’t be split apart. If you agree with them, you can’t cheat and tear the /dʒ/ piece in two to make words with /d/ and /ʒ/- neither of which are in either mintor sage on their own.
- You’re making a word with these sounds, so you have to remember what order you pulled them out in. If you pulled /m/, /e/, and /s/ but didn’t remember what order they came in, you haven’t really made a word. That may seem obvious, but it matters for the math.
If you have a collection of objects and you’re taking some to all of them and putting them in an order, that’s called a permutation. Permutations, among other things, are studied in the field of math known as combinatorics. For a set of N (whatever non-negative integer, or whole number, you want) objects, you can make N! permutations of those objects. N! is read Nfactorial, which means N times N-1 times N-2 times… and so on, until you get to 'times 3 times 2 times 1’.
The nice thing about this way of making blends is that there probably aren’t any or many blends that can’t be made this way, with enough time and patience. That is, this method or model (probably) doesn't undergenerate: there are no real-life examples that the model can’t account for.
The problem is, this method sucks. N! is a really big number- find a calculator that can graph and calculate factorials and use it to graph Y = X!. That’s a steep upwards curve if I’ve ever seen one. For example, between mintand sage there are seven sounds. 7! is 5,040. What if you wanted to blend, say, skeletonwith titties? That’s thirteen sounds, and 13! is 6,227,020,800- over six billion 'possible’ blends in this model.
Why is this a problem? I don’t know about you all, but when I sit down to make a blend- like you do- I usually come up with maybe three, five max, blends that seem reasonable, and usually I settle on one that really works. And when I mentioned the bone titties meme on an imageboard, the person who responded to me took no time at all to coin the word skeletittiesfrom skeletonand titties- not the response time of someone who’s sifting painstakingly through six billion options trying to find the best one.
So, while treating blends as permutations of the handful of sounds that make up the words they’re made of doesn't undergenerate, it does overgenerate wildly- it labels 'possible’ blends that wouldn’t actually be made in the real world. It’s like a floodlight, it’ll illuminate the target… and everything around it, too. We want a spotlight that will only light up the star onstage- the real-world blends. How can we manage that?
There’s one simple way to narrow the beam that’s probably a good idea anyway. Consider: nstm /nstm/ is a possible blend in the permutation model, but it’s not a possible word in the English language. If someone tried to tell you about this new word nstm, your first response would probably be 'Gesundheit.' nstm violates the phonotactics of English, the rules about what sounds can be next to what other sounds and, as a result, what novel combinations of sounds can qualify as English words. For instance, words in English always contain some kind of vowel sound*, which nstm conspicuously lacks. So what if we just crossed off the list of permutations any 'blend’ that couldn’t be a word in the English language?
This is a start, but there are plenty of permutations that could be words but are really terrible blends. For mintand sage,mastin /'me.stɪn/ comes to mind. It’s definitely a possible word, but I don’t think I would produce that if I was trying to blend those words. So there must be some greater regularity to blends that our model just doesn’t capture. What might some of those regularities be? We’ll find out next time.
*This is both true and not-true, and I can hear some of you wincing right now as I’m typing it. On the phonetic level, it’s false: some syllables in English, instead of being built around a vowel, are built around a nasal, /ɹ/ (English’s R-sound), or /l/. See, for instance, button['bʌ.ʔn̩],rhythm [ˈɹɪðm̩], batter ['bæ.ɾɹ̩] (or ['bæ.ɾɚ]), and bottle ['bɑ.ɾɫ̩]. The undertick marks these syllabic consonants that, despite not being vowels, take the nucleus or core position usually associated with vowels. However, this can only occur in unstressed syllables (where vowel reduction, in which vowels are produced with less energy and often less distinctly, also occurs) and a pronunciation with [ə] in front of the consonant in question is always possible in addition to the syllabic consonant pronunciation. This leads most linguists to say that underlyingly, that is on the phonemic level, the words have a schwa in the nucleus that gets reduced further to zero, moving the /m/, /n/, /ɹ/, or /l/ into the nucleus. So phonologically, in English anyway, there really is always a vowel in there somewhere.
This talk was given by Elizabeth Kelley at our student combinatorics seminar. She cited Godbole, Kurtz, Pralat, and Zhang as collaborators. One of these (Pralat, I think) was originally an editor, but then made substantial contributions to the project. This post is intended to be elementary.
[ Personal note: This is the last talk post I will be writing for OTAM. It seems fitting, since Elizabeth and I went to the same undergrad; I have actually known her for almost as long as I have been doing mathematics. ]
——
Acquisitions Incorporated
This is a graph theory talk, but, refreshingly, it did not begin with “Agraph is a pair of vertices andedges such that…”
It did begin with this: Let $G$ be a graph with a vertex-weighting (i.e. an assignment of nonnegative reals to each vertex). An acquisition move is a “complete transfer of weight” from a low-weight vertex to an adjacent higher-weight vertex. In other words, if the weights before the move are $w\leq x$, then the weights after the move are $0\leq w+x$ (respectively).
[ For the sake of not cluttering up the definitions with trivialities, we will say that both of the weights involved in an acquisition move must be strictly positive— that is: not zero. ]
From this, a bunch of definitions follow in quick succession.
- A sequence of acquisition moves is called an acquisition protocol if it is maximal, i.e. after performing all of the moves, no further move is possible.
- The set of nonzero-weight vertices after performing an acquisition protocol is called a residual set.
- Finally, the acquisition number of $G$ is the minimum size of any residual set. We write it as $a(G)$.
This explains half of the title. The other half of the title, is perhaps a bit more self-explanatory. A lot is known about acquisition numbers when, say, all vertices are given weight $1$. Less is known in other contexts, but the goal of this paper is to ask what we “should” expect for paths. More precisely: if we give the vertices random weights, what is the expected acquisition number?
——
Fekete’s Lemma
A sequence of real numbers $(x_n)$ is called subadditive if it does what the name suggests: for all $n$ and $m$
$$ x_{n+m} \leq x_n + x_m.$$
This is a pretty general construction, and tons of sequences do this: certainly any decreasing sequence will, and also most reasonable sequences that grow slower than linear ($\log(n)$ works, for instance). Usually, when the situation is so general, it is hard to say anything at all about them, but in this case things are different:
Lemma (Fekete). Given any subadditive sequence $(x_n)$, the limit of $x_n/n$ exists, and moreover
$$ \lim_{n\to\infty} \frac{x_n}{n} = \text{inf}_n \frac{x_n}{n}. $$
(This lemma has one of my favorite proofs, which is essentially the same as the one given in this NOTSB post; just reverse all the inequalities and repeat the argument with liminf/limsup replaced by lim/inf.)
This means that whenever you have a subadditive sequence, it makes sense to ask about its growth rate, which is just the limit that Fekete guarantees exists. Less formally, it is the number $c$ such that $x_n \approx cn$ as $n$ gets large. (Perhaps in this formulation is the existence statement so striking: why should there be such a number at all? But Fekete states that there is.)
As it happens, it is pretty easy to prove that $a(P_n)$, where the path $P_n$ on $n$ vertices has been weighted with all 1s, forms a subadditive sequence.
This proof doesn’t use much about the weightings at all: it requires only that they are “consistent” in some technical sense. The punchline for our purposes is that $a(P_n)$ continues to form a subadditive sequence when the paths are weighted by independent identically distributed random variables.
——
Numbers, Please!
In the paper, Kelley considered the case when the vertex weights were distributed as a Poisson distribution. This is a thing whose details aren’t too important, but if you’re familiar with it you may be wondering why this instead of anything else? The answer is because when you know the answer for the Poisson model, you also know it in a more physically reasonable model: you start with a fixed amount of weight and you distribute it randomly to the vertices.
[ The process by which you use Poisson to understand the latter model is called “dePoissonization”, which makes me smile: to me it brings to mind images of someone hunched over their counter trying to scrub the fish smell out of it. ]
But enough justification: what’s the answer? Well, we don’t actually know the number on the nose, but here’s a good first step:
Theorem (Godbole–Kelley–Kurtz–Pralat–Zhang). Let the vertices of $P_n$ be weighted by Poisson random variables of mean $1$. Then $0.242n \leq \Bbb E[a(P_n)] \leq 0.375n$.
The proof of this theorem is mostly number-crunching, except for one crucial insight for each inequality: This step is easier to prove for the lower bound: after we have assigned numbers for the random variables, check which functions have been given the weight zero and look at the “islands” between them. Acquisition moves cannot make these islands interact, and so we can deal with them separately, so $\Bbb E[a(P_n)]$ splits up into a sum of smaller expectations based on the size of the islands. In a strong sense “most” of the islands will be small, and so you get a pretty good approximation just by calculating the first couple terms.
To get an upper bound, you need to think of strategies which will work no matter low long the path is and what variables are used. The most naïve strategy is to just pair off vertices of the path and send the smaller one in the pair to the larger one. This may or may not be an acquisition protocol, but you will always cut the residual set size (roughly) in half. Following even this naïve strategy is good enough to give the 0.375.
Both of these steps are fairly conceptually straightforward, but it becomes very difficult to calculate all the possibilities as you get further into the sum; in other words, it’s a perfect problem for looking to computer assistance. This allows us to get theoretical bounds $0.29523n \leq \Bbb E[a(P_n)] \leq 0.29576n$; and of course it would not be hard to get better results by computing more terms, but at some point it’s wiser to start looking for sharper theoretical tools rather than just trying to throw more computing power toward increasingly minuscule improvements.
This talk was given by Jay Yang as a joint talk for this year’s CA+ conference and our usual weekly combinatorics seminar. He cited Daniel Erman as a collaborator.
——
Ein–Lazarsfeld Behavior
Yang began the talk with a fairly dense question: what is the asymptotic behavior of a Betti table? He then spent about 20 minutes doing some unpacking.
What is a Betti table? This has an “easy” answer, which is that it is an infinite matrix of numbers $\beta_{ij}$ defined as $\dim \text{Tor}^i(M)_j$, but this is maybe not the most readable thing if you’re not very well-versed in derived functors. Fortunately, exactly what the Betti table is is not super important for understanding the narrative of the talk.
But, for the sake of completeness we briefly give a quote-unquote elementary description: Given a module $M$, produce its minimal free resolution— that is, an exact sequence $\cdots\to F_2\to F_1\to F_0\to M\to 0$, where $F_i$ are all free, and the maps, interpreted as matrices, contain no constant terms. If $M$ is a graded module over a graded ring, then the $F_i$ are also graded, and so we can ask for a basis for the submodule of (homogeneous) elements of degree $j$. This number is the Betti table entry $\beta_{i,j}$.
What do we mean by asymptotic? We need to have something going off to infinity, clearly, but exactly what? There are several ways to answer this question: one which Yang did not explore was the idea of embedding by degree-$n$ line bundles, and sending $n\to\infty$. Instead of doing that, we will force our modules $M$ to come from random graphs, and then take asymptotic to mean sending the number of vertices to infinity.
What do we mean by behavior? Again, Yang deviates from the usual path: the most well-studied kind of long-term behavior is the “$N_p$” question “For how long is the resolution linear?” But instead of doing this, we will discuss the sorts of behaviors which were analyzed by Ein and Lazarsfeld.
One of these behaviors, which he spent most of the time talking about, concerns the support of the table, and stems from their 2012 result:
Theorem (Ein–Lazarsfeld). If $X$ is a $d$-dimensional smooth projective variety, and $A$ a very-ample divisor, then
$$ \lim_{n\to\infty} \frac{ \# \text{nonzero entries of the } k^\text{th} \text{ row of } X_n}{\text{projdim}(X_n) + 1} = 1$$
where $X_n$ is the homogeneous coordinate ring of $X$ embedded by $nA$, and $1\leq k\leq d$.
The same limit formula was reached in 2014 and 2016 for different classes of rings than $X_n$.
Ein and Lazarsfeld also showed another kind of asymptotic behavior together with Erman in a similar situation: namely, that the function $f_n$ sending $i$ to a Betti table element $\beta_{i,i+1}(S_n/I_n)$ converges to a binomial distribution (after appropriate normalization).
Yang examined both of these behaviors to see if they could be replicated in a different context: that of random flag complexes.
——
Random Flag Complexes
Arandom graph is, techncially speaking, any random variable whose output is a graph. But most of the time when people talk about random graphs, they mean the Erdős–Rényi model of a random graph, denoted $G(n,p)$:
Any graph consists of vertices and edges. So pick how many vertices you want ($n$), and then pick a number $0\leq p\leq 1$ which represents the probability that any particular edge is in the graph. Then take the complete graph on $n$ vertices, assign independent uniform random variables, and remove each edge whose output is larger than $p$.
This gives rise to the notion of an Erdős–Rényi random flag complex, denoted $\Delta(n,p)$, by taking a $G(n,p)$ and then constructing its flag complex:

(source)
And finally, we can describe a Erdős–Rényi random monomial ideal, denoted $I(n,p)$ by taking a $\Delta(n,p)$ and then constructing its Stanley-Reisner ideal.
The punchlines is that $I(n,p)$ will, in nice cases, exhibit the Ein-Lazarsfeld behaviors:
Theorem (Erman–Yang). Fix $r>1$ and $F$ a field. Then for $1\leq k\leq r+1$ and $n^{-1/r} \ll p \ll 1$, we have
$$ \lim_{n\to\infty} \frac{ \# \text{nonzero entries of the } k^\text{th} \text{ row of } F[x_1,\dots, x_n]/I(n,p)}{\text{projdim}(F[x_1,\dots, x_n]/I(n,p)) + 1} = 1,$$
where the limit is taken in probability
Theorem (Erman–Yang). For $0<c<1$ and $F$ a field, the function sequence $(f_n)$ defined by
$$ f_n(i) = \Bbb E \Big[\beta_{i,i+1}(F[x_1,\dots, x_n]/I(n,p)\Big]$$ converges to a binomial distribution (after appropriate normalization).
The latter statement can be made considerably stronger, eliminating expected values in exchange for requiring convergence in probability. But he stated it in this generality so that he could concluded the talk by giving proof sketches for both statements (which I won’t reproduce here).
This talk was given by Lauren Williams at this year’s CA+ conference. She cited Reitsch has her collaborator. (It was not the winner of this conference; I had to miss the winning talk, unfortunately.)
Her talk was pretty fast, and in the end there was still more to talk about than she had time for. In particular, she frequently alluded to the cluster algebra stuff going on in the background but we never explicitly talked about it. Also, she explicitly said that she wanted to “downplay” the mirror symmetry. My impression from this, and what snippets I’ve gotten from other people, is that mirror symmetry seems to be very hard to explain in a convincing way.
In any case, she spent the first half of the talk laying out a detailed outline, without defining too much. This post will pretty much follow that outline exclusively; leaving out the more detailed explicit combinatorial constructions involving plabic graphs. In particular, this means I’ll be skipping a lot of definitions, so this post will not be elementary.
——
NObodies
The surviving words in the title are Newton–Okounkov bodies and Grassmannians. The latter is fairly easy to describe if you feel good about linear stuff: the Grassmannian $\text{Gr_d}(\Bbb C^n)$ is the collection of all $d$-dimensional subspaces of the vector space $\Bbb C^n$.
[ Of course there is a lot more that one can say about the Grassmannian, but that won’t be necessary here. ]
TheNewton-Okounkov body is one of those combinatorial constructions that I said I was going to leave out, but let me try to give some general flavor. Given a toric variety, we can construct a thing called the “moment polytope”; this turns out to be pretty darn useful for understanding toric varieties. The Newton-Okounkov body $\Delta$ (or NObody) is an object defined in an attempt to produce similarly nice geometric objects for arbitrary varieties.
[ NObodies, in particular, need not be polytopes, in which case a lot of the good combinatorics from moment polytopes isn’t accessible. But all of the NObodies associated to Grassmannians turn out to be polytopes, and so the dream is still alive. ]
So if we are going to want to talk about NObodies, there had better be some varieties hanging around. These varieties are the images of a map $(\Bbb C^\times)^N \to \text{Gr}_{n-k}(\Bbb C^n)$ which is defined with the help of a particular kind of plabic graph. We’ll denote the NObody of such a thing by $\Delta_G$, where $G$ is the corresponding plabic graph.
The lattice points of $\Delta_G$ tell us something about the geometry of the relevant Grassmanian. More specifically, if we scale $\Delta_G$ by a factor of $r$, the integer lattice points of $r\Delta_G$ turn out to define a basis for the space of sections $H^0(X,\mathcal O(rD))$, where $D$ is the ample divisor $\{P_{1,2,\dots, n-k}=0\}$.
All of this lives on the “A model” side of the mirror symmetry construction. On the other side of the mirror, something different happens.
——
Bee Model
The A model gets all of its power from the Grassmannian, and there is an analogous shape that governs everything in the B model as well. This shape isn’t much harder to describe, but it is a little more technical: it is the subset of $\text{Gr}_k(\Bbb C^n)$ containing those subspaces for which every cyclic Plücker coordinate is nonzero. And a cyclic Plücker coordinate is the determinant of every $k\times k$ submatrix containing columns $i+1, i+2,\dots, i+k$, where the $(n+1)^\text{th}$ row is the first row, and so on).
Because of an even shorter and more technical way to describe this shape (the complement of the anticanonical divisor) there exists a function mapping it to $\Bbb C(x)$ called the superpotential, which she very intentionally said nothing about. I’ve written briefly about something called a “superpotential” as part of one of the combinatorics seminar talks. This had the advantage that we actually defined the darn thing, but still the same problem that we don’t really know what this thing is for. It must be one of those things where it’s not so easy to say.
Analogous to $\Phi_G$ in the A model is a different map called the cluster chart $\Psi_G$, also defined by a plabic graph $G$. This defines coordinates on the B model shape, and so we can try to write the superpotential in terms of those coordinates. If you do this, you get a polynomial map, and if you tropicalize that map, the resulting graph is a polytope. We denote that polytope by $Q_G$.
——
The Miracle
Those of you who have done enough mathematics (even if it doesn’t have anything to do with this stuff), probably know what’s coming next:
Theorem (Reitsch–Williams, 2015). For a fixed plabic graph $G$,
$$ \Delta_G = Q_G. $$
The fact that $\Delta_G$ and $Q_G$ are related at all is not obvious. The constructions are very different from one another: one comes from a NObody associated to walks on the plabic graph, and the other comes from a tropicalization of the superpotential.
But what is even more amazing is that they’re not just related: they are equal. And Williams said this in no uncertain terms: equal means equal. Like, as sets. No combinatorial equivalence, or rescaling, or isometry, or anything. And I dunno about you, but I find that pretty miraculous.
This talk was given by Alex Yong at this year’s CA+ conference. He cited Robichaux as a collaborator, as well as high school student Anshul Adve.
——
Factorial Schur Functions
As with all the best combinatorics, we start with a game.
Given a partition (possibly with some zero parts), draw its Young diagram but replace the boxes with black dots and the “positions without boxes” with white dots. Don’t have any extra rows, but extra columns are okay. For instance, the partition $(2,2,0)$ corresponds to this picture
We then make moves according to the following rule, anytime we see a black dot in a TL corner of a square that’s otherwise white, we can move it to the BR corner:
We make this move wherever possible until there are no more available. The set of all diagrams that can be obtained this way, starting with the partition $\lambda$ will be called, uncreatively, $\text{Black}(\lambda)$. To keep with our example, here is $\text{Black}((2,2,0))$:
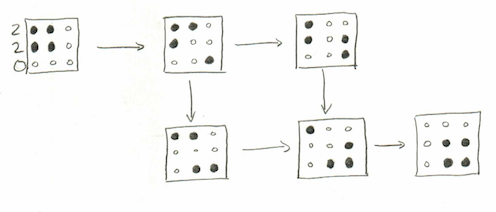
Now it is time for some algebra: we are going to describe a polynomial in two sets of variables $X=x_1,\dots, x_r$, where $r$ is the number of rows; and $Y=y_1, y_2, y_3,\dots$ representing the columns. First, we define the weight of a diagram $\text{wt}(D)$ to be the product of every $x_i-y_j$, for all $i$ and $j$ such that there is a black dot in row $i$ and column $j$.
Finally, define the factorial Schur function $s_\lambda(X,Y)$ to be the sum of $\text{wt}(D)$ over all diagrams $D\in\text{Black}(\lambda)$. As a formula:
$$ s_\lambda(X,Y) = \sum_{D\in\text{Black}(\lambda)} ~~ \prod_{(i,j)\text{ is black}} x_i-y_j. $$
——
Littlewood-Richardson Polynomials
The reason that factorial Schur functions are called that is because if you plug $y_i=0$ for every $y$, the resulting polynomial is really, honestly, the Schur polynomial. Schur functions form a basis for the symmetric algebra, and so we might hope that the symmetric Schur functions are the basis for something. This hope turns out to be validated: it is a $\Bbb Z[Y]$-module basis of $\Lambda_n\otimes \Bbb Z[Y]$ (The last symbol there is polynomial algebra in the $y$-variables, and the symbol in the middle is a tensor product)
Because of that, this means that $s_\lambda(X,Y)s_\mu(X,Y)$ must be some linear combination, and so we can ask for the structure coefficients $C_{\lambda,\mu}^\nu(Y)$. We write the $Y$ there because in general these things can be an element in $\Bbb Z[Y]$; in other words, can be a polynomial in the $y$-variables.
Since they specialize to the Littlewood-Richardson coefficients when $y_i=0$, we call these $C_{\lambda,\mu}^\nu$ the Littlewood-Richardson Polynomials
[ Because of the geometric interpretation of ordinary Littlewood-Richardson coefficients, we know that they are nonnegative integers; you may ask whether the LR-polynomials are also positive (in that all the coefficients are negative). The answer is no, but they are positive as polynomials in $z_i:=y_{i+1}-y_i$. ]
——
Polynomial Time
In 2005, one day after the other, two papers were posted to the arXiv, both claiming to have proven the following theorem:
Theorem (DeLoera–McAllister 2006, Mulmuley–Narayanan–Sohoni 2012*). There is an algorithm for determining whether or not the Littlewood-Richardson coefficient $c_{\lambda,\mu}^\nu=0$ in polynomial time.
If you’re not super familiar with “polynomial time”, feel free to substitute the word “quickly” anywhere you see it; this isn’t necessarily true but it’s a respectable approximation.
This naturally raises the question of whether the Littlewood-Richardson polynomials can also be determined to be zero or not in polynomial time. As the title of the talk suggests— and as Adve, Robichaux, and Yong proved— the answer is yes. The rest of this section is devoted to a proof sketch.
There is a celebrated proof due to Knutson–Tao which proves the so-called saturation conjecture, that $c_{\lambda,\mu}^\nu=0$ if and only if $c_{N\lambda,N\mu}^{N\nu}=0$ for all $N$. At this point, Yong talked a little bit about the history of that conjecture:
- In the 19th century, people were asking this question about Hermetian matrices.
- In 1962 Horn conjectured a bunch of inequalities which resolved the question.
- In 1994 Klyachko solved the problem, but didn’t use Horn’s inequalities.
- Soon after, it was realized that the saturation conjecture was sufficient to prove Horn’s inequalities.
- In 1998, Knutson and Tao published their proof.
The argument they made in this paper was refined by a 2013 theorem of a different ARY team: Anderson, Richmond, and Yong. They showed that the analogous statement is true for the Littlewood–Richardson polynomials: $C_{\lambda,\mu}^\nu(Y)=0$ if and only if $C_{N\lambda,N\mu}^{N\nu}(Y)=0$ for all $N$.
The major innovation made by the new ARY team (Adve, Robichaux, and Yong) constructed a family of polytopes $P_{\lambda,\mu}^\nu$ with the following properties:
- scaling the polytope by a factor of $N$ is the same as scaling the partitions by a factor of N, i.e. $P_{N\lambda,N\mu}^{N\nu} = NP_{\lambda,\mu}^\nu$,
- and the crucial bit: $P_{\lambda,\mu}^\nu$ has an integer lattice point if and only if $C_{\lambda,\mu}^{\nu}(Y)\neq 0$
In particular, this implies that the “polynomial saturation conjecture” can be used to reduce the question of $C_{\lambda,\mu}^{\nu}(Y)\neq 0$ to figuring out whether $P_{\lambda,\mu}^\nu$ is the empty polytope. And this, finally, is a problem which is known to be solvable in polynomial time, which concludes the proof.
——
[ * The dates listed above are the publication dates of the papers that the two teams wrote. “So that tells you something about publishing in mathematics”, Yong says. Perhaps, but… I’m not sure what. I’m assuming that what he was getting at is this: The names in the latter team are nothing to scoff at, by a long shot; I mean, I have heard all five of these names before in other contexts. But the prestige associated to the names in the former team might have made that paper subject to less scrutiny than the latter. Or perhaps he just meant that the capricious turns of fate can turn what “should be” a short procedure into a long one. ]
This post represents the second half of a talk given by Emine Yildirim at our combinatorics seminar.
If you’ve not already read the first one, you don’t technically have to, as long as you’re happy assuming that there are special posets associated to each Coxeter group called “cominiscule”. But it will probably be more rewarding if you read the posts in order.
In any case, this post will make really no attempt at all to be elementary.
——
Excuse Me, Which Algebra?
We wish to consider a path algebra, and so we need to have a directed graph. You might imagine that we would just use the Hasse diagrams of the posets which we just drew, with some orientation thrown on. That’s a very reasonable guess; it just happens to not be what Yildirim did.
Instead she first considers the set of order ideals (which are all subsets of poset elements which are “downward closed”: if $x$ is in the subset then every $a\leq x$ must also be in the subset) of a cominiscule poset. Since order ideals are, in particular, subsets of the same set, the collection of all order ideals come with their own natural order structure— namely, inclusion of sets.
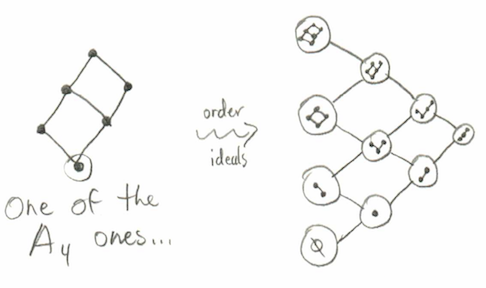
[ Eagle-eyed viewers may notice what one of the members of the audience pointed out: this poset structure is actually a cominiscule poset itself (for type C). After some consideration, we decided that this is probably a coincidence; the order ideal poset of cominiscule posets will not in general be cominiscule. ]
We take the Hasse diagram of that poset (e.g. as drawn above), interpret it as a graph with the edges as directed downward, and finally take the path algebra of that(whew!). We will call such an algebra $\mathcal A$, suppressing the dependence on the cominiscule root. Note that this directed graph is acyclic, and so $\mathcal A$ is finite-dimensional.
In any case, the goal is to prove the following:
Conjecture. The Auslander-Reiten translation $\tau$ has finite order $2(h+1)$ on the Grothendeick group of the bounded derived category of $\textbf{Mod}(\mathcal A)$.
So there’s lots of words here but the point is that that Yildirim was able to prove this conjecture for all the cominiscule posets… except the triangular poset that comes from types C and D. So it’s technically still a conjecture, but she solved a substantial portion of it, and so I will still refer to “Yildirim’s proof.”
In the remainder of the post, we make an attempt to explain why this might be true, and why the Coxeter transformation has anything to do with anything.
——
“Bounded Derived Category”?
I will not attempt to define the bounded derived category construction, but I will tell you an important fact abut it: it is “derived” in the sense that its objects are chain complexes $\to A \to B\to C\to$, but all of the quasi-isomorphisms are invertible.
This bit of abstract nonsense means that we can replace any $\mathcal A$-module $M$ by its minimal projective resolution:
$$ 0 \to P_{n}\to \cdots \to P_{2}\to P_{1}\to P_{0} \to 0. $$
[ Here we are using the “homological” definition of a projective resolution, where $M$ does not show up in the sequence itself but rather is isomorphic to the kernel of the last map. It’s not super important. ]
In the post based on Yildirim’s pre-talk, we pointed out that the defining characteristic of the Coxeter transformation is that it “turns projectives into injectives”. One can define the Coxeter transformation so that it does this functorially, i.e. in such a way that we get a sequence
$$ 0 \to I_{n}\to \cdots \to I_{2}\to I_{1}\to I_{0} \to 0. $$
This turns out to be an injective coresolution of any module $N$ (“co” meaning that $N$ is the of the kernel of the second map), and we say that the Coxeter transformation turns $M$ into $N$.
Update: actually things are even worse than I thought: in general this does not even have to be an injective resolution! (Thanks @yildirimemine (!!) for the correction.)
——
The Key Lemma
The Coxeter transformation is a useful tool for understanding the Auslander-Reiten translation $\tau$, but there is a major hurdle to making it any more useful than just using $\tau$ itself.
A module $M$ of a path algebra coming from a Hasse diagram is called an interval if it arises as a quiver representation in the following way:
- choose an “upper” vertex $\beta$ and a “lower” vertex $\alpha\leq\beta$,
- for each vertex $v$ between these two, i.e. satisfying $\alpha\leq v\leq\beta$, place a copy of the field $k$ at $v$, and
- place the zero map at every edge between any two vertices.
Then the Coxeter transformation need not take intervals to intervals.
However, Yildirim’s proof of the conjecture relies on the following discovery.
Lemma. For all $\mathcal A$ except the one arising from the triangular poset, there exists a collection of intervals which are taken to intervals. Moreover, these form a basis for the (relevant) Grothendieck group.
Again these are words, but they have a practical effect. Namely, any module $M$ can be broken down into pieces, each of which is an interval that is taken to an interval. So, roughly speaking, as long as we understand the Coxeter transformation on such modules, we understand the Coxeter relation in general.
[ In light of the Update, this becomes even more remarkable: some intervals are not even taken to resolutions! And yet somehow there is this nice collection we can carve out that not only is taken to resolutions, but even resolutions of intervals…]
Because of this, and because of the Coxeter transformation’s close connection to the Auslander-Reiten translation, she is able to understand the latter in a more stripped-down form, without its full algebraic trappings. This, finally, she uses to prove the conjecture. The difficulty with the single remaining family of posets is that we do not (yet?) have such a basis.
[Previous ] [ Post 3 ]
So, for reasons [explained below the break*], it occurred to me that the deadline for submitting abstracts to the Joint Meetings is probably pretty soon (it is— September 26— so if you’re planning to submit, better get your ass in gear!). And while I was looking through the sessions, I was once again reminded why I flinging love the Joint Meetings.
Here are some actual titles of sessions— sessions!There will be multiple talks on these things!
- AMS Special Session on Set-theoretic Topology (Dedicated to Jack Porter in Honor of 50 Years of Dedicated Research)
- MAA Invited Paper Session on Quandle Questions
- EXCELLENT??
- Also:Alissa Crans giving an MAA Invited Address(!) on “Quintessential Quandle Queries”
And there’s a bunch of “mathematical practice” sessions
- MAA Session on Philosophy of Mathematics as Actually Practiced
- Short version for the unaware: there has recently been a growing trend in philosophy of mathematics to shift the discipline closer to studying the practices of professional mathematicians.
- This is basically everything I like about philosophy plus everything I like about anthropology/sociology (I’m really bad at distinguishing the two) thrown together into a big pot and seasoned liberally with modern math; delicious!
- AMS Special Session on Alternative Proofs in Mathematical Practice
- Besides just being generically interesting, the title of this session is based on the title of a book that came out recently (which is really darn expensive, sorry). So I’m interested to see how the session interacts with that.
- MAA Session on Good Math from Bad: Crackpots, Cranks, and Progress
- OH MY WORD
- YAAAASSSSSSSSS
- (If you thought i had forgotten about that post, LOL no. I’m gonna teach that class someday. Just you watch.)
Also:
- AMS Special Session on Boundaries for Groups and Spaces
- this… has to be intentional, right?
- that’s the thing about this kind of math humor: you never know if the person was being clever, or if they’re just so far gone down the rabbit hole that they forget what words mean.
- under the assumption that it’s intentional, A+
- AMS Special Session on A Showcase of Number Theory at Liberal Arts Colleges
- This one’s a little subtle. If this were by the MAA, this would be whatever. But it’s not: it’s by the AMS. This is very outside the usual AMS fare and I’m hoping that it succeeds because that would indicate that at least one of teaching, undergrad research, and non-R1 research are being actively supported by both major American mathematical communities, which… fucking finally.
And then there are all the the sessions I’m excited about because people! Math friends!
- AMS Special Session on Research from the Rocky Mountain-Great Plains Graduate Research Workshop in Combinatorics
- AMS Special Session on Research in Mathematics by Early Career Graduate Students
- People like me except marginally better at not procrastinating? yes please?
- (Also it’s an AMS Special Session so there’s definitely some expectation of quality there… at least with the work. With the presentation style… we’ll see.)
- AMS Special Session on Special Functions and Combinatorics (in honor of Dennis Stanton’s 65th birthday)
- Oh shit that guy taught me combinatorics!
- Happy birthday Dennis! Whenever it happens to be!
- is there any polite way to ask when a professor’s birthday is?
anD SPEAKING OF PEOPLE:
- MAA Invited Address — Transforming Learning: Building Confidence and Community to Engage Students with Rigor by Maria Klawe
- ARE YOU KIDDING ME
- She is the president of my undergrad and that is the least of the many reasons I love her.
- MAA Project NExT Lecture on Teaching and Learning — Changing Mathematical Relationships and Mindsets: How All Students Can Succeed in Mathematics Learning by Jo Boaler
- NO FUCKING WAY
- Jo Boaler is a relentless advocate of IBL techniques in the K12 setting
- And in particular wrote What’s Math Got To Do With It? that book was my bible on math ed for a good three years, dam.
- AMS Invited Address — Algebraic Structures on Polytopes by Federico Ardilla
IS IT JANUARY YET?!?!?!
——
* So an idea I’ve had kicking around for a little while is that maybe I could try to take some of the lessons that I’ve learned from writing this blog and give a little contributed talk at the Joint Meetings this year. I’ve never really thought to do this earlier because it just doesn’t feel right to eat up a spot just to do some cheap advertisement. But I think I’m more comfortable with the idea now, since I’ll be several months out from writing the blog by then, and I don’t have a follow-up project planned. I mean, I do, it’s called “writing my damn thesis already”, but I haven’t figured out how to publicize that yet* :P
Part of the reason I want to do this is definitely because I’d love the blog to “count” for something CV-wise, and a contributed presentation at a conference isn’t much but it isn’t nothing.
But another reason is that over the course of my writing OTAM is that I’ve talked with a lot of people in real life who speak longingly about blogging. It’s something they’ve wanted to do for a while— maybe they even did do it for a month or two— but have never really found the time/drive/whatever. And I’ve never really had anything useful to say to comments like this. I think that the effort of preparing a conference talk might force me to straighten out my perspective on the value of this whole enterprise, which I think would allow me to have more meaningful conversations.
(This sounds rather falsely noble, but it’s also a bit self-serving: I suspect that I’ll find myself being one those people ten years from now, if not for blogging then for something else. It would be nice to have something of value to say to future-me, too.
[ * I thought pretty seriously about streaming thesis work. But in the end I came to the conclusion that I would need a much more flexible camera setup so that I could film my paper, or alternatively to get some kind of comfortable whiteboard setup in my room. The issue is that it’s easy to stream TeX, but I can’t do all my actual work in TeX; I need some flexibility to draw faster than I can TikZ. So I got myself a cheap tablet (and wow, that’s a story: ask me about it IRL sometime) thinking that I could get used to drawing on that. But in the end I really just couldn’t; I haven’t figured out how to think on the tablet the way I can think on paper or whiteboards**. I have no doubt that I could learn to do it, but I also have no particular interest in learning right now. ]
[ ** Unpopular opinion: chalkboards are great for teaching and giving talks, but when I do math that I have to actually think about, whiteboard every time. ]
