#potential plane
Beyond Descartes - Part 9:
The Potential Plane
and Probable States of Change
Composite Dimension and
Amplitudes of Potentiality
Episode 3

(continued from here)
We have seen that an imaginary number is a complex number that can be written as a real number multiplied by the imaginary unit i, which is defined by its property ixi =−1. The square of an imaginary number bi is −b2. For example, 6i is an imaginary number, and its square is −36.[1] Other than 0, imaginary numbers yield negative real numbers when they are squared.[2]
Turning now to potential numbers, we can similarly define a unit of potentiality p by the property p x -p = -1. [Long pause here waiting for the other shoe to drop.] Just a minute, you say, that’s just like 1 x -1 = -1. Yes, it is. And that is just the point. All real numbers. Nothing to imagine. And Descartes finally vindicated after all these years - imaginary numbers just imaginary after all. But how does this work? Or does it even work? What exactly is the point? Is this a joke? It’s no joke, I assure you. It’s an easier and better way to achieve the same ends - - - and more. Muchmore.
The secret is in the sauce, I say slyly. Really? Well, yes - in a way. Though imaginaries use a sauce with nearly identical ingredients. The recipe is p + (-p) = 0. And, of course, i + (-i) = 0 as well. The trick is in how - - - and where - - - the sauce is applied. In the potential plane the sauce is applied more liberally in more locations for greater lubrication.
Levity aside. (This is after all a TST[3].) The complex plane uses a single axis. This axis represents a new dimension, wholly distinct from the x, y and z dimensions. Strangely, we’re never informed where this axis/dimension might be located, just that it is somewhere other than where x, y and z are located. Stranger still, the complex plane allocates the y-axis of the Cartesian plane for its own use in location of its points. Although never specifically mentioned, to my knowledge, I surmise the imaginary dimension exists in what mathematics and physics both call phase space.[4]
The mandalic or potential plane uses no such underhanded plan. It openly posits the existence of six new dimensions, allocated equally with two accompanying each of the Cartesian dimensions, all overtly evident. (All nine spatial dimensions in plain sight together, that is.) Nothing left to the imagination. As the new dimensions are made commensurate with the old in a hybrid geometric display, no imaginary dimension is needed. Coordinates of all potential dimensions are readily communicable with the real number system through all of the ordinary Cartesian dimensions concurrently along with the Cartesian coordinates. Moreover, mandalic geometry conjectures that the ordinary Cartesian dimensions may in fact originate in interactions among number species of potential dimensions filtered through impacts on inherited biological sensory mechanisms.[5] This raises yet another interesting possibility.[6]
In the long convoluted history of mathematics, the imaginary numbers were introduced as a correlative to the number line with its real numbers. That meant, among other things, that they were linear, consisting of a single dimension. The complex plane related the two
in a kind of hybrid geometry that consisted of one real dimension and one imaginary dimension. Mathematician William Rowan Hamilton in 1843 proffered the quaternions, a number system that extends the complex numbers to three dimensions, whereupon things went, to my mind, from bad, to very much worse.
Quaternions came with certain dysfunctional characteristics, among them, the fact that multiplication of two quaternions is noncommutative. This is problematic. The imaginary and complex numbers, at least, had both been commutative. Nevertheless, physics endorsed the quaternions as it earlier had imaginary and complex numbers.
Why? Because the quaternions do in fact give partly correct results, and when investigating a dimly illuminated region of reality, such as the subatomic world still is today, even partial results are heartily welcomed if that is all that can be had. The sad consequence of this, is that physics has been led astray in its quest for truth for over a century now, because partial truths can be much more misleading than complete errors. Total error is often uncovered much sooner than partial truth, which can pass undiscovered, depending upon circumstances, for a very long time.
Mandalic geometry will be shown to be free of the difficulty posed by noncommutative multiplication. It is fully commutative throughout its nine dimensions (three ordinary, six extraordinary). It was not composed that way from a number line, with elements that could be commutatively multiplied with one another. It came that way fully formed from the start, in its primeval embodiment as a multidimensional structure, expressing behavior intrinsic to holistic nature.
Next time around, we’ll begin to look under the hood of the mandalic approach to geometry and see if we can grokit.
(continuedhere)
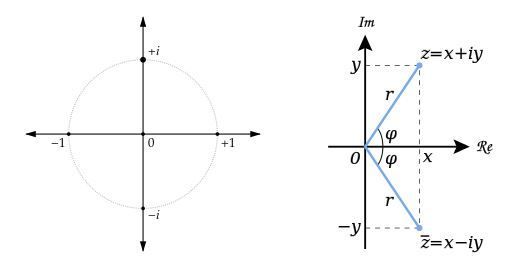
Image: (lower left) Imaginary unit i in the complex or Cartesian plane. Real numbers lie on horizontal axis, imaginary numbers on the vertical axis. By Loadmaster (David R. Tribble), (Own work) [CC BY-SA 3.0orGFDL], via Wikimedia Commons; (lower right) A diagram of the complex plane. The imaginary numbers are on the vertical axis, the real numbers on the horizontal axis. By Oleg Alexandrov [GFDLorCC-BY-SA-3.0],via Wikimedia Commons
Notes
[1] 62xi2 = 36 x (-1) = -36.
[2] Zero (0) is considered both real and imaginary, and both the real part and the imaginary part are defined as real numbers. (If that makes little sense to you, don’t blame me. I’m just the messenger here, reporting what the mathematicians have stated to be the case.) This seems to me to be purely an arbitrary definition, and it confuses me as much as it probably does you. Could it be they did this to avoid the situation where 02 x (-1) = -0? I think I would find that definition less disturbing, welcome even.
[3] Newly coined Internet acronym for Truly Serious Topic. (Not to be confused with TSR Totally Stupid Rules.)
Speaking about “greater lubrication”(wewere a moment ago, remember?), I use the phrase not simply as a figure of speech, or a simile, but rather, as a metaphor. "Spicing" of mandalic geometry with all those zeros of potentiality makes for a very “fluidic dish” which, I believe, reflects the changeable nature of reality far better than the stricter, strait-laced coordinates of Descartes or the complex plane are able to do. And it’s not just a matter of fluidity involved here. The mandalic form so begotten is, in fact, a probability distribution through the three Cartesian dimensions concurrently, which feature alone makes mandalic geometry an ideal candidate for application to quantum physics.
[4] A phase space of a dynamical system is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space. In a phase space every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system (that is to say, any allowed combination of values of the system’s parameters) a point is included in the multidimensional space. [Wikipedia]
[5] I am speaking here of the hybrid 6D/3D formulation of mandalic geometry which combines the features of dimensional numbers, potential numbers, and composite dimension, this being a fully open access geometric system that has nothing hidden, nothing held back. What you see is what you get. (WYSIWYG)
[6] It is tempting to wonder whether there might be a close connection between the composite dimensions/potential coordinates proposed by mandalic geometry and the pilot wave theoryorde Broglie–Bohm theory of quantum mechanics. At least there seems to be a correlation between David Bohm’s implicate/explicate order and the manifest/unmanifest (potential) coordinates of mandalic geometry.
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 285-
Beyond Descartes - Part 8:
A Good Convention Gone Bad,
An Opportunity Missed
Composite Dimension and
Amplitudes of Potentiality
Episode 2


(continued from here)
We cannot blame Descartes for imaginary numbers. It was he, after all, who christened these numbers “imaginary” due to his disdain for them. We can, however, fault him for his lack of insight into how his coordinate system could be extended to create a viable substitute to show that imaginary numbers and the complex plane were nonsensical and make them unnecessary. Alas, that was not to be. Certain powerful forces of history decreed that imaginary numbers were here to stay and we seem stuck with them still, nearly five centuries later.
Not all would agree that imaginary numbers are a bad convention. We should all, however, be able to agree that they are a convention and nothing more. They were invented by humanity.[1] Mathematics may not have taken to them at first - but did eventually welcome them into its fold for better or worse. The real damage was done when physics did the same without first subjecting the mathematical concepts involved to the kind of scrutiny and empirical review it demands of its own theories.
Where is the proof that imaginary numbers and complex plane in fact apply to the real world and particularly to the subatomic realm? It is lacking in the main, and though the geometric concepts have indeed been successfully applied to a number of branches of physics and explanations of a variety of physical phenomena, the reconciliation is incomplete, the fit an uncomfortable one, and too many mysteries remain unexplained.
The term imaginary unit refers to a solution to the equation x2 = -1. By convention, the solution is usually denoted i. As no real number exists with this property, the imaginary number i extends the real numbers and creates an entirely new and different category of numbers. And crucially, at this point an assumption is made, a rather sweeping assumption. It is assumed that the properties of addition and multiplication we’re familiar with - (closure, associativity, commutativity and distributivity) - continue to hold true for this new species of number, or I should say, for this newly derived artificial species of number. That may fly in the ivory tower[2] of pure mathematics, but it lacks the wings and propelling force required to maneuver effectively in the real world that physics investigates. Still, the complex plane, generated by mathematically motivated minds, was soon adopted by physicists the world over.[3]
Mandalic geometry offers an alternative solution in the effective combination of dimensional numbers, composite dimension, and plane of potentiality. We’ll take a close look at potential numbers first. Let’s see how they stack up against the imaginary numbers, how and where they differ. Distinctions between complex plane and potential plane are subtle but they make for a world - a universe, actually - of difference. When next we meet, kindly check all preconceptions at the door. Entirely untrodden paths await.
(continuedhere)
Image: (lower left) Imaginary unit i in the complex or Cartesian plane. Real numbers lie on horizontal axis, imaginary numbers on the vertical axis. By Loadmaster (David R. Tribble), (Own work) [CC BY-SA 3.0orGFDL], via Wikimedia Commons; (lower right) A diagram of the complex plane. The imaginary numbers are on the vertical axis, the real numbers on the horizontal axis. By Oleg Alexandrov [GFDLorCC-BY-SA-3.0],via Wikimedia Commons
Notes
[1] Let those who suppose differently, who believe them to be an indelible part of nature itself, prove their case. Until they do, I will see fit to call such numbers manmade inventions.
[2] I use the term ivory tower without malice of any kind in this context, rather judiciously, because mathematics demands no more than internal consistency for its particular brand of truth. It is not much interested in examining its definitions and axioms to determine how they shape up against hard reality. Mathematicians leave that "sordid work" to physicists and philosophers, both of whom are more willing to dig in the mire of nature, seeking its actual relics. Enthusiastically to persist in such a real world-oblivious manner as pure mathematicians do, I think, requires a very special type of mind, one I don’t fully understand myself.
[3] In some circles this would be considered no less than a monumental leap of faith, particularly in view of the many unproved assumptions made in creation of imaginary and complex numbers. This was, in fact, the New Faith promulgated by Descartes’ contemporaries, the rationalists of the Age of Reason, to supplant the Old Faiths of Religion and Scholasticism.
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 284-
Beyond Descartes - Part 5
Reciprocation, Alternation, Decussation
Imaginary and Complex Numbers

(continued from here)
Previously in this blog a number of attempts have been made to explicate the Taoist number line and contrast it with the Western version of the same. It is essential to do this and to do it flawlessly, first because different systems of arithmetic result from the two, and secondly because the mandalic coordinate system is based on the former perspective while the Cartesian coordinate system is based on the latter.[1]
What has been offered earlier has been accurate to a degree, a good first approximation. Here we intend to present a more definitive account of the Taoist number line, describing both how it is similar to and how it differs from the Western number line used by Descartes in formation of his coordinate system. This will inevitably transport us well beyond that comfort zone offered by the more accessible three-dimensional cubic box that has heretofore engaged us.
Both Taoist and Western number lines observe directional locative division of their single dimension into two major partitions: positive and negative for the West; yinandyang for Taoism.[2] There the similarities essentially end. From its earliest beginnings Taoism recognized a second directional divisioning in its number line, that of manifest/unmanifestorbeingandbecoming.[3] The West never did such. As a result, some time later the West found it necessary to invent imaginary numbers.[4][5]
Animaginary number is a complex number that can be written as a real numbermultiplied by theimaginary uniti, which is defined by its property i2 = −1. [Wikipedia]
Descartes knew of these numbers but was not particularly fond of them. It was he, in fact, who first used the term “imaginary” describing them in a derogatory sense. [Wikipedia] The term “imaginary number” now just denotes a complex number with a real part equal to 0, that is, a number of the form bi. A complex number where the real part is other than 0 is represented by the form a + bi.
In place of the complex plane, Taoism has (and always has had from time immemorial) a plane of potentiality. An explanation of this alternative plane was attempted earlier in this blog, but it can likely be improved. This post has simply been a broad brushstrokes overview. In the following posts we will look more closely at the specifics involved.[6]
(continuedhere)
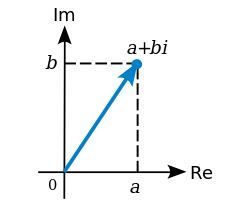
Image (lower): A complex number can be visually represented as a pair of numbers (a, b) forming a vector on a diagram representing the complex plane. “Re” is the real axis, “Im” is the imaginary axis, and i is the imaginary unit which satisfies i2 = −1. Wolfkeeper at English Wikipedia [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons
Notes
[1] The arithmetic system derived from the Taoist number line can perhaps best be understood as a noumenal one. It applies to the world of ideas rather than to our phenomenal world of the physical senses, but it may also apply to the real world, that is, the real real world which we can never fully access.
Much of modern philosophy has generally been skeptical of the possibility of knowledge independent of the physical senses, and Immanuel Kant gave this point of view its canonical expression: that the noumenal world may exist, but it is completely unknowable to humans. In Kantian philosophy, the unknowable noumenon is often linked to the unknowable “thing-in-itself” (Ding an sich, which could also be rendered as “thing as such” or “thing per se”), although how to characterize the nature of the relationship is a question yet open to some controversy. [Wikipedia]
[2] From the perspective of physics this involves a division into two major quanta of charge, negative and positive, which like yinandyang can be either complementary or opposing. Like forces repel one another and unlike attract. This is the basis of electromagnetism, one of four forces of nature recognized by modern physics. But it is likely also the basis, though not fully recognized as such, of the strong and weak nuclear forces, possibly of the force of gravity as well. I would suspect that to be the case. The significant differences among the forces (or force fields, the term physics now prefers to use) lie mainly, as we shall see, in intricate twistings and turnings through various dimensions or directions that negative and positive charges undergo in particle interactions.
[3] It is this additional axis of probabilistic directional location, along with composite dimensioning, both of which are unique to mandalic geometry, that make it a geometry of spacetime, in contrast to Descartes’ geometry which, in and of itself, is one of space alone. The inherent spatiotemporal dynamism that is characteristic of mandalic coordinates makes them altogether more relevant for descriptions of particle interactions than Cartesian coordinates, which often demand complicated external mathematical mechanisms to sufficiently enliven them to play even a partial descriptive role, however inadequate.
[4] In addition to their use in mathematics, complex numbers, once thought to be "fictitious" and useless, have found practical applications in many fields, including chemistry, biology, electrical engineering, statistics, economics, and, most importantly perhaps, physics..
[5] The Italian mathematician Gerolamo Cardano is the first known to have introduced complex numbers. He called them “fictitious” during his attempts to find solutions to cubic equations in the 16th century. At the time, such numbers were poorly understood, consequently regarded by many as fictitious or useless as negative numbers and zero once were. Many other mathematicians were slow to adopt use of imaginary numbers, including Descartes, who referred to them in his La Géométrie, in which he introduced the term imaginary, that was intended to be derogatory. Imaginary numbers were not widely accepted until the work of Leonhard Euler (1707–1783) and Carl Friedrich Gauss (1777–1855). Geometric interpretation of complex numbers as points in a complex plane was first stated by mathematician and cartographer Caspar Wessel in 1799. [Wikipedia]
[6] What I have called here the plane of potentiality occurs only implicitly in the Taoist I Ching but is fully developed in mandalic geometry. It may be related to bicomplex numbers or tessarines in abstract algebra, the existence of which I only just discovered. Unlike the quaternions first described by Hamilton in 1843, which extended the complex plane to three dimensions, but unfortunately are not commutative, tesserines or bicomplex numbers are hypercomplex numbers in a commutative, associative algebra over real numbers, with two imaginary units (designated i and k). Reading further, I find the following fascinating remark,
The tessarines are now best known for their subalgebra of real tessarines t = w + y j, also called split-complex numbers, which express the parametrization of the unit hyperbola. [Wikipedia]
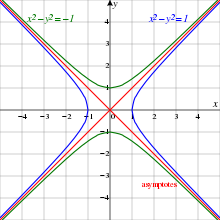
The rectangular hyperbola x2-y2 and its conjugate, having the same asymptotes. The Unit Hyperbola is blue, its conjugate is green, and the asymptotes are red. By Own work (Based on File:Drini-conjugatehyperbolas.png) [CC BY-SA 2.5],via Wikimedia Commons
Note to self: Also investigate Cayley–Dickson constructionandzero divisor. Remember, this is a work still in progress, and if a bona fide mathematician believes division by zero is possible in some circumstances, (as is avowed by mandalic geometry), I want to find out more about it.
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 281-
