#complex numbers

Can a number system be both the new kid on the block and older than written history?

The real number system as it exists today has been with us for a few centuries.  In foundation it is monovalent,  monophasic,  and sequential.

The probable number system dates to prehistory but was lost in the mists of time until recently rediscovered and resurrected.  In contrast to the real number system it is foundationally bivalent, biphasic, and cyclic.

The probable number system has considerably more structure than the real number system and is therefore more robust.  In this sense, it is similar to the complex number system.

In contrast to the complex number system,  the probable number system in its foundation presupposes that numbers can assume wavelike forms capable of  constructive and destructive interference  operationally through the compositing of higher to lower dimension.

By means of compositing of dimension probable numbers are able to  distribute  throughout the entire  mandalic unit vector cube  (which is structurally a  superposition  of  the 6-dimensional unit vector hypercube on the 3-dimensional unit vector cube) a function analogous in important ways  to that performed in the complex number system by the centralized imaginary unit i.

Another important way in which the probable number system differs from both the real number system and the complex number system is the absence of  nothingness  and the zero representing it.  In its place we find the concepts of  balance and equilibrium.  Nullification still exists in form of annihilation and its opposite in the form of creation.  But the Cartesian coordinate system  of ordered pairs and ordered triads  is transformed by this approach to handling number and dimension  from a ring into a field of hyperdimensional numbers over real numbers in three dimensions.

(to be continued)

© 2016 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 315-

Magic Theatre: For Madmen Only

If we describe a Cartesian ordered triad by x,y,z we can describe an analogous 6-dimensional ordered sextuplet  or 6-tuple  by x_a,y_a,z_a,x_b,y_b,z_b

The definitions that translate a 6-dimensional ordered sextuplet (hexagram in Taoist terminology) into a 3-dimensional ordered triad (trigram in Taoist terminology) are:^[1]

• (x_a + x_b) / 2 = x
• (y_a + y_b) / 2 = y
• (z_a + z_b) / 2 = z

I think the methodology will work for all scalar quantities. But as currently formulated,  mandalic geometry (MG) is a discrete geometry based entirely on unit vectors.  We are talking about the line segments between -1 and +1 in the various dimensions and only points -1, 0, and +1 in each line segment in Cartesian terms.

In essence we are not yet particularly concerned with scalars here but only with vectors :  -, +, and neutral (0).

Mathematically √−1 is important because by adding it to the real number field, as we have done, we create the algebraically complete field of complex numbers. In mathematics, a complete field is a field equipped with a metric and complete with respect to that metric. The real numbers and complex numbers are both complete fields. Cartesian coordinates- - - ordered pairs and ordered triads- - - although based on real numbers,  do not form a field. This has important implications, implications which can be ignored only at peril to the particular conceptual system involved..

The definitions above all give three possible results in Cartesian terms: -1, 0, +1.  Remember though MG hybridizes six dimensions with three dimensions and represents them superimposed. Wherever one or more zeros occurs in Cartesian coordinates we have also corresponding 6-dimensional forms,  composed of just +1s and -1s,  of which there are always two for each Cartesian zero.  A Cartesian ordered triad with one zero is associated with two such 6-dimensional forms; an ordered triad with two zeros, with four; an ordered triad with three zeros (the origin), with eight. An ordered triad without zeros will have only one associated 6-dimensional form.  This constitutes the mandalic pattern, which is an essential feature of the 6D/3D formulation of this geometric system and isomorphism naturally comes into play here as well.

Andthat is how and why all numbers in this coordinate system based on higher-dimensional extensions of the real numbers “square” to numbers which can be  either positive or negative  and then reduce or "collapse" to corresponding Cartesian forms that preserve the same sign. This is a necessary result of the fact that a primary “zero form” in
6-dimensional terms is lacking,  only +1s and -1s exist.  These can then interfere constructively and destructively as number waves, to produce a  "secondary zero"  by destructive interference  whenever linked forms differ in sign in one or more paired dimensions. Since the two linked 6-dimensional numbers are always inverse to one another, any Cartesian zero then can be substituted with two such 6-dimensional forms. This is the process that makes imaginary numbers unnecessary, replacing them with two inversely related probable numbers which behave in most ways like real numbers  and  are  distributed  throughout the entire geometric system.

“Hybridization” is probably not the best term here but will be used until I can think of a better descriptor. What I intend is not actual joining and unification,  but rather  a superposition and conceptual commingling in three-dimensional terms. Such a representational mapping substitutes for all Cartesian forms  "equivalent" forms  containing only 1s and -1s, no zeros.  In so doing, it effectively converts the Cartesian coordinate system from just a ring to a field as well, properly interpreted. Basically then, the probable numbers do for the real numbers much the same as the complex numbers do,  but with even greater and more utilitarian results which are also more easily managed.

In operational terms, complex numbers perform two rather simple binary operations: a scaling and a rotation. Scaling capability is clearly inherited through its real number lineage; rotational capacity, from its imaginary number lineage.  Together,  scaling and rotation combine to augment or diminish an axis of growth and produce vector ambulation in a circular path about a central origin point of reference.  The scaling factor  could be said to detemine the  radius of revolution;  the rotation factor, the angle of revolution. And that’s pretty much all there is to the “great mystery”  of complex numbers.  Their importance  resides in the great number of fields of endeavor where the combination of these two superpowers is necessary and/or convenient.

Nature uses this combination of scaling and rotation in many of its processes.  Atomic and subatomic proceedings  are probably not among these.  How then did it come about that  quantum mechanics  arrived at the notion that  rotation and scaling  could be applicable to modeling of discontinuos states of being?  Both refer to changes through continuous space. I think it was an accident of history. In 1925, Erwin Schrödinger, in his search for a way to explain  certain mysteries then perplexing the greatest physicists of the day,  hit upon his  eponymous equation  which appeared to do the trick.  So well,  in fact,  that quantum mechanics has been  justly considered  the single most successful description of reality ever devised. And the equation that basically accomplished this success involves the imaginary number i and complex numbers.^[2]

An important aspect of the operation of rotation, one which may have bearing on the Schrödinger equation and its huge success, has been largely overlooked. The result of a rotation can often mimic the result of inversion (reflection through a point), making the two indistinguishable by measurement alone. To someone wearing a blindfold there is no way to tell whether i has by the operations of squaring and rotation changed itself into  -1  or  -1,  the inversion element of multiplication,  has simply reflected  +1,  the identity element of multiplication,  through the origin point to  -1.  Explaining away a 90° rotation with a right angle reflection will no doubt prove more difficult but let’s not just yet deny that it might be doable.

Could there be a way to reformulate the Schrödinger equation then so it contains no imaginary or complex numbers?  Many have tried to do that very thing and failed. No one has succeeded in nearly a century. Still, we might wonder if the time is ripe now to remove the blindfold. Perhaps we might do well to inquire whether quantum physics is, in some manner we don’t quite understand, a victim of its own success.

In theory, circumventing use of complex numbers in a defining equation of quantum mechanics should be possible. On what basis do I say this?  The equation we have now relies on complex numbers.  These in turn derive an ability to produce rotation from the imaginary number √−1 .  But there are  other mathematical means  to accomplish the same. Trigonometry comes most immediately to mind. The circle and cyclicity it models have a very long and distinguished history. Complex numbers as we’ve noted can also produce scaling.  But so can real numbers.  And close examination reveals  that complex numbers inherit their ability to scale from the two real numbers they contain. The hard truth ultimately is  there is nothing all that special  about  complex numbers  or complex plane. Possibly it is their utilitarian ease of use that positions them as an attractive methodology. Other routes to ease of use exist as well. There is always more than one way to skin the proverbial cat  (even a cat residing only in the mind of a physicist named Schrödinger.)

Consider also, how great is the actual need for scaling in quantum mechanics?  The distance from  centermost part of the atom  to the outer reaches of electron orbital space is in fact quite small.  Furthermore,  the elements of this universe of discourse are quantized,  so actual distances involved are moot.  In the extreme,  the question persists  as to  whether “distance” is a concept even applicable  in this context  of quantum logic. Quantum numbers  themselves  range between 0 and 2.  I can count the allowed values on the fingers of one hand.

Regarding rotation, where exactly does that come into play in the quantum realm?  Electrons do not orbit the nucleus of the atom.  They jump from orbital to orbital by discretized changes in energy involving photon exchange. In the nucleus it seems such discretized instanteous changes take place as well,  obviating any need for rotation.  Obviously physics misguided here by labeling one of the quantum numbers “spin”. Sometimes a rose is best referred to as a rose. The problem here is that we don’t really know what it is that “spin” refers to.

The quintessential equation of quantum mechanics was formulated by a physicist, not a mathematician. It is not a simple algebraic equation, but in general a linear partial differential equation,  describing the time-evolution of the system’s wave function (“state function”). “Derivations” of the Schrödinger equation  do generally demonstrate its mathematical plausibility for describing wave-particle duality. To date, however, there are  no universally accepted derivations  of Schrödinger’s equation from appropriate axioms.  Nor is there any  general agreement  as to what the equation actually signifies.  Moreover, some authors have demonstrated that certain properties  emerging from Schrödinger’s equation  can even be deduced from symmetry principles alone.  This would appear to be a worthwhile direction of investigation to pursue.  Quantum mechanics is most fundamentally about symmetry.  Let’s make Emmy Noether proud by giving her the recognition she deserves.

Finally, it was not without considerabledifficulty that Schrödinger developed his equation.  In the end,  it almost seems  he pulled it out of a hat,  as a magician might a rabbit.^[3]   Part of the  Zeitgeist  of the physics community  in the early 1920s  revolved around  the peculiar notion  that particles  behaved as waves.  Schrödinger decided to follow this direction of thought  and  find an appropriate 3-dimensional wave equation for the electron. His equation succeeded beyond his wildest dreams.  Adopted in the canon of  the new physics,  it became the cornerstone of that radically different physics, changed forever. Physics has never looked back since.

Still, one startling and haunting fact persists: nowhere else in all of physics  has it ever been found necessary to invoke complex numbers.

Once,  quite a long time ago,  I believed  imaginary numbers  were wrong. I was the one that was wrong. Later, having grown a little more clever, I came to think that √−1 was a necessary evil- - -correct but not validly applicable to quantum physics. Wrong again. Currently it is my belief that imaginary numbers are guilty of an even worse offense: both true from the mathematical standpoint and partly applicable to physics. The worst of both worlds.  Yielding results that are in large part correct, imaginary and complex numbers have managed to lead us all down the garden path for the better part of a century. Have we then gone past the point of no return?  My contention  is  that it is possible to complete the ring that Cartesian coordinates present  and  transform it to a field over the real numbers, with appeal only to higher-dimensional analogues of the reals and no need for imaginary or complex numbers,  an approach which, if actually possible, would offer certain undeniable advantages.^[4]

Essentially the method of composite dimension does away with i and complex numbers by distributing an operation analogous to that of i throughout six dimensions or three in Cartesian terms and then working with same by means of reflections (inversions) only. So an algebra based on the system necessitates use of only the real numbers and their higher dimension extensions that I have called probable numbers.  Only simple addition and multiplication  are required.  For those in the audience who are "sufficiently mad”, there is the added bonus that a kind of division by zero becomes possible. We’ll find out soon enough whether you qualify.

A few additional explanatory remarks are in order here:

Depending on the variant,  Cartesian geometry (CG),  represents space in two or three dimensions. Points in the former are referenced to two pairwise perpendicular axes; in the latter, to three.

Because Descartes assumes as axiomatic a 1:1 correspondence of number to spatial location each of his three axes becomes a facsimile of the number line, only in different dimensions.

Mandalic geometry (MG) approaches representation of space differently, using a hybrid coordinate system which relates a higher dimension space to a lower dimension space  with a 2:1 correlation.

Itcan be represented entirely commensurate with CG, but in so doing a “glass slipper effect” occurs. Just as Cinderella’s stepsisters can manage to force a too fat foot into her glass slipper, the results leave something to be desired.  In our context here,  the  "something to be desired"  is a clear and full understanding of six-dimensional reality in its own right. We end up interpreting it in time-sharing terms of probabilities and randomness.

What Descartes refers to as an ordered pair requires two higher dimension ordered pairs to represent in MG; a Cartesian ordered triad requires three higher dimension ordered pairs to represent in MG.

In Taoist terminology the notational equivalent of a Cartesian ordered pair is a  "bigram",  a two-line symbol,  each line of which  can take one of two values. As a result there are four types of bigram. Two bigrams make up a tetragram; three, a hexagram.

Descartes views a point as having only two essential characteristics:

• It is dimensionless.
• It is just a location in space which can be uniquely represented
  by a single ordered pairorordered triad.

Mandalic geometry rejects both of these axioms. It regards a point, or a particle so represented, as an evanescent entity emerging from interaction of two higher dimensions expressed in our world of three dimensions in such limited manner.

Thiscan be represented in context of Cartesian space but in making mandalic coordinates commensurate with Cartesian coordinates it is no longer possible to represent every “point” in space uniquely with a single mapping of number to location.  What results instead is the probabilistic distribution pattern of the mandala, which we,  from our limited vantage in spacetime, misinterpret as something it is not.

MG is a discrete geometry. The result of the mapping formula used is a mandalic configuration in which the 3-dimensional cube composed of  unit vectors in Cartesian space  becomes a  "probability distribution"  in combined mandalic space.

I have placed the quotation marksaroundprobability distribution because this is a perspective that arises  from our inability to see all that is involved accurately. I suspect this has repercussions pertinent to a full comprehension or grokking of quantum mechanics and possibly of string theory as well.

Since the 64 discrete “points” of  the unit vector hypercube of six dimensions represented by the hexagrams cannot “fit” simultaneously in the 27 discrete points of the 3-dimensional unit vector cube  by any representational method available to our inherited bio-psychocultural mechanism, a sort of time-sharing process occurs in observations and measurements of reality which we interpret in terms of probability.

What has been described here occurs at enormous velocities close to that of light, and likely refers only to processes in the subatomic quantum realm. For MG, which is also a hybridization of mathematics and physics, context is always of the essence.

There is much more to be said in explanation of mandalic geometry. I see, though, this post has already run rather long, so we will end it here. Enough has already been said in way of introduction of basic material.

Notes

[1] Since the coordinate system is describing a cube with an n-hypercube superimposed,  there is an additional constraint placed on all coordinates in
the 6-tuples.  All scalar values must be identical for x, y and z values.  That constraint assures that all vectors though they may differ in sign (direction) maintain equal magnitudes.

When the 6-tuples are dimensionally reduced to 3-tuples by the method I’ve called “compositing of dimension”  the resulting geometric figure consists of four different dimensional amplitudes of 6-tuples collapsed.  The amplitudes of dimension correspond  in spatial terms  to the vertices,  edge centers,  face centers and cube center. The pattern that emerges is that of a mandala. This is a highly symmetric pattern though all symmetries aren’t necessarily apparent immediately, even using Taoist notation. The probability distribution of the 6-tuples allots the hexagrams in the following manner:  one to each vertex;  two to each edge center; four to each face center; one to the cube center. The result is  placement of 64 6-tuples  in 27 positions of discrete 3-tuples  in the specific mandalic distribution pattern described.

Think here of the analogy of a hydrogen atom confined within a cubic space of specified side length determined by the nuclear and atomic force fields. The single electron,  existing in such quantized energy levels that are possible,  can assume various different locations in different orbital shells,  but every location in a given orbital must be equidistant from the nuclear proton. Once reduced by dimensional compositing the 6-tuples described here fill four distinct shells that have different radii or distances from the center.  From center to periphery these distances can be described as zero;  one (or square root one);  square root 2; and square root 3. (Pythagorean theorem)

[2] Schrödinger was not entirely comfortable with the implications of quantum theory. About the probability interpretation of quantum mechanics that came out of Solvay ‘27 he wrote:  "I don’t like it,  and I’m sorry I ever had anything to do with it.“ ["A Quantum Sampler”. The New York Times. 26 December 2005.]

[3] In later years another great physicist, Richard Feynman, would remark, “Where did we get that (equation) from? Nowhere. It is not possible to derive it from anything you know. It came out of the mind of Schrödinger.”

[4] A different approach to avoiding the need for complex numbers from the one I am suggesting is described here. To my mind it offers little of value other than an interesting alternative explanation of what complex numbers are and do. A similar conclusion seems to have been reached by the author.

© 2016 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 313-

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - IV

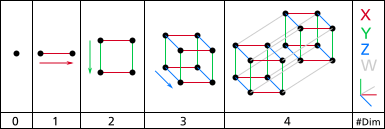
(continued from here)

One of the notable things the Rationalists  failed to take into account in their analysis and codification of square roots  was  the significance of context. In so doing they assured that all related concepts they developed would eventually degenerate into a series of errors of conflation.  Do  not ever underestimate the importance of context.

Mathematicians, for example, can show that for any 3-dimensional cube  there exists  a  2-dimensional square,  the area of which equals the volume of the cube.^[1] And although that is true, something has been lost in translation. This is another of the sleights of hand mathematicians are so fond of.  Physicists cannot afford to participate in such parlor tricks as these, however mathematically true they might be.^[2]

We will begin now, then, to examine how the mandalic coordinate approach stacks up against that of imaginary numbers and quaternions. The former are holistic and respective of the natural order; the latter are irresponsibly rational, simplistic and, in final analysis, wrong about how nature works.^[3] Ambitious endeavor indeed, but let’s give it a go.

We’ve already looked at how the standard geometric interpretation of imaginary numbers in context of the complex plane is based on rotations through continuous Euclidean space.  You can brush up on that aspect of the story here if necessary. The mandalic approach to mapping of space is more complicated and far more interesting.  It involves multidimensional placement of elements in a discrete space, which is to say a discontinuous space,  but one fully commensurate with both Euclidean and Cartesian 3-dimensional space. The holo-interactive manner in which these elements relate to one another leads to a  probabilistic mathematical design  which preserves commutative multiplication,  unlike quaternions which forsake it.

Transformations between these elements are based on inversion (reflection through a point) rather than rotation which cannot in any case reasonably apply to discrete spaces.  The spaces that quantum mechanics inhabits are decidedly discrete.  They cannot be accurately detailed using imaginary and complex numbers or quaternions.  To discern the various, myriad transitions which can occur among mandalic coordinates requires some patience. I think it cannot be accomplished overnight but at least in the post next up we can make a start.^[4]

(continuedhere)

Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions  (A tesseract).  There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

Notes

[1] If only in terms of scalar magnitude. Lost in translation are all the details relating to vectors and dimensions in the original.  Conflation does not itself in every case involve what might be termed ‘error’ but because it always involves loss or distortion of information,  it is nearly always guaranteed to eventuate in error somewhere down the line of argument. The point of all this in our context here is that, in the history of mathematics, something of this sort occurred when the Rationalists of the Enlightenment invented imaginary and complex numbers and again when quaternions were invented in 1843. These involved a disruption of vectors and dimensions as treated by nature. The loss of information involved goes a long way in explaining why no one has been able to explain whyandhow quantum mechanics works in a century or more.  These  misconstrued theses  of mathematics behave like a demon or ghost in the machine that misdirects,  albeit unintentionally, all related thought processes.  What we end up with is a plethora of confusion. The fault is not in quantum mechanics but in ourselves, that we are such unrelentingly rational creatures, that so persistently pursue an unsound path that leads to reiterative error.

[2] Because physicists actually care about the real world; mathematicians, not so much.

[3] It must be admitted though that it was not the mathematicians who ever claimed imaginary numbers had anything to do with nature and the real world. Why would they? Reality is not their concern or interest. No, it was physicists themselves who made the mistake. The lesson to be learned by physicists here I expect is to be careful whose petticoat they latch onto. Not all are fabricated substantially enough to sustain their thoughts about reality, though deceptively appearing to do just that for protracted periods of time.

[4] My apologies for not continuing with this here as originally intended. To do so would make this post too long and complicated. Not that transformations among mandalic coordinates are difficult to understand,  just that they are very convoluted. This is not a one-point-encodes-one-resident-number plan like that of Descartes we’re talking about here. This is mandala country.

© 2016 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 309-

Beyond Descartes - Part 5

Reciprocation, Alternation, Decussation
Imaginary and Complex Numbers

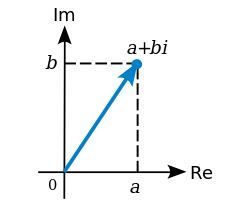
(continued from here)

Previously in this blog a number of attempts have been made to explicate the Taoist number line and contrast it with the Western version of the same.  It is essential to do this and to do it flawlessly,  first because different systems of arithmetic result from the two, and secondly because the mandalic coordinate system is based on the former perspective while the Cartesian coordinate system is based on the latter.^[1]

What has been offered earlier has been accurate to a degree, a good first approximation. Here we intend to present a more definitive account of the Taoist number line,  describing both how it is similar to and how it differs from the  Western number line  used by Descartes in formation of his coordinate system.  This will inevitably transport us  well beyond that comfort zone offered by the more accessible three-dimensional cubic box that has heretofore engaged us.

Both Taoist and Western number lines observe directional locative division of their single dimension into two major partitions:  positive and negative for the West;  yinandyang for Taoism.^[2]  There the similarities essentially end.  From its earliest beginnings Taoism recognized a second directional divisioning in its number line, that of manifest/unmanifestorbeingandbecoming.^[3]  The West never did such.  As a result, some time later the West found it necessary to invent imaginary numbers.^[4][5]

Animaginary number is a complex number that can be written as a real numbermultiplied by theimaginary uniti, which is defined by its property i² = −1. [Wikipedia]

Descartes knew of these numbers but was not particularly fond of them.  It was he, in fact, who first used the term “imaginary” describing them in a derogatory sense. [Wikipedia]  The term “imaginary number” now just denotes a complex number with a real part equal to 0,  that is, a number of the form bi. A complex number where the real part is other than 0 is represented by the form a + bi.

In place of the complex plane, Taoism has (and always has had from time immemorial)  a plane of potentiality.  An explanation of this alternative plane was attempted earlier in this blog,  but it can likely be improved. This post has simply been a broad brushstrokes overview. In the following posts we will look more closely at the specifics involved.^[6]

(continuedhere)

Image (lower): A complex number can be visually represented as a pair of numbers (a, b) forming a vector on a diagram representing the complex plane. “Re” is the real axis, “Im” is the imaginary axis, and i is the imaginary unit which satisfies i² = −1. Wolfkeeper at English Wikipedia [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons

Notes

[1] The arithmetic system derived from the Taoist number line can perhaps best be understood as a  noumenal  one. It applies to the world of ideas rather than to our phenomenal world of the physical senses, but it may also apply to the real world, that is, the real real world which we can never fully access.

Much of modern philosophy has generally been skeptical of the possibility of knowledge independent of the physical senses, and Immanuel Kant gave this point of view its canonical expression: that the noumenal world may exist, but it is completely unknowable to humans. In Kantian philosophy, the unknowable noumenon is often linked to the unknowable “thing-in-itself” (Ding an sich, which could also be rendered as “thing as such” or “thing per se”), although how to characterize the nature of the relationship is a question yet open to some controversy. [Wikipedia]

[2] From the perspective of physics this involves a division into two major quanta of charge, negative and positive, which like yinandyang can be either complementary or opposing.  Like forces repel one another and unlike attract. This is the basis of electromagnetism, one of four forces of nature recognized by modern physics. But it is likely also the basis, though not fully recognized as such, of the strong and weak nuclear forces, possibly of the force of gravity as well. I would suspect that to be the case. The significant differences among the forces  (or force fields, the term physics now prefers to use)  lie mainly, as we shall see, in intricate twistings and turnings through various dimensions or directions that negative and positive charges undergo in particle interactions.

[3] It is this additional axis of probabilistic directional location, along with composite dimensioning, both of which are unique to mandalic geometry, that make it a geometry of spacetime,  in contrast to Descartes’ geometry which, in and of itself, is one of space alone. The inherent spatiotemporal dynamism that is characteristic of  mandalic coordinates  makes them altogether more relevant for descriptions of particle interactions than Cartesian coordinates, which often demand complicated external mathematical mechanisms to sufficiently enliven them to play even a partial descriptive role, however inadequate.

[4] In addition to their use in mathematics, complex numbers, once thought to be  "fictitious" and useless,  have found practical applications in many fields, including chemistry, biology, electrical engineering, statistics, economics,  and, most importantly perhaps, physics..

[5] The Italian mathematician Gerolamo Cardano is the first known to have introduced complex numbers. He called them “fictitious” during his attempts to find solutions to cubic equations in the 16th century.  At the time, such numbers were poorly understood,  consequently regarded by many as fictitious or useless as negative numbers and zero once were. Many other mathematicians were slow to adopt use of imaginary numbers, including Descartes, who referred to them in his La Géométrie, in which he introduced the term imaginary,  that was intended to be derogatory. Imaginary numbers were not widely accepted until the work of Leonhard Euler (1707–1783) and Carl Friedrich Gauss (1777–1855).  Geometric interpretation of  complex numbers as points in a complex plane  was first stated by mathematician and cartographer Caspar Wessel in 1799. [Wikipedia]

[6] What I have called here the plane of potentiality occurs only implicitly in the Taoist I Ching but is fully developed in mandalic geometry. It may be related to  bicomplex numbers  or tessarines in abstract algebra, the existence of which I only just discovered. Unlike the quaternions first described by Hamilton in 1843, which extended the complex plane to three dimensions, but unfortunately are not commutative,  tesserines or bicomplex numbers  are hypercomplex numbers in a commutative,  associative  algebra over real numbers,  with two imaginary units (designated i and k). Reading further, I find the following fascinating remark,

The tessarines are now best known for their subalgebra of real tessarines t = w + y j, also called split-complex numbers, which express the parametrization of the unit hyperbola. [Wikipedia]

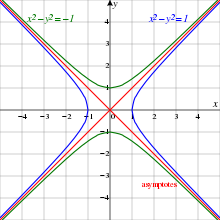
The rectangular hyperbola x2-y2 and its conjugate, having the same asymptotes. The Unit Hyperbola is blue, its conjugate is green, and the asymptotes are red. By Own work (Based on File:Drini-conjugatehyperbolas.png) [CC BY-SA 2.5],via Wikimedia Commons

Note to self:  Also investigate Cayley–Dickson constructionandzero divisor. Remember,  this is a work still in progress,  and if a  bona fide mathematician  believes division by zero is possible in some circumstances,  (as is avowed by mandalic geometry), I want to find out more about it.

© 2015 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 281-