#quaternions

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - V

(continued from here)

The four Cartesian quadrants provide the two-dimensional analogue of the number line and its graphic representation in Cartesian coordinate space.  This is the true native habitat of the square and, by implication, of square root.  Because  Enlightenment mathematicians  found fit to define square root in a different context inadvertently  -that of the number line- we will find it necessary to devise a different name for what ought rightly to have been called square root,  but wasn’t.  I propose that we retain the existent definition of tradition and refer to the new relationship between opposite numbers in the square,  that is to say,  opposite vertices through two dimensions or antipodal numbers, as contra-square root.^[1]

Modified from image found here.

Given this fresh context - one of greater dimension than the number line - it soon becomes clear with little effort that a unit number^[2]ofany dimension multiplied by itself gives as result the identity element of that express dimension. For the native two-dimensional context of the square the identity element is OLD YANG,  the bigram composed of two stacked yang (+) Lines,  which corresponds to yang (+1),  the identity element in the  one-dimensional context  of the number line. In a three-dimensional context,  the identity element is the trigram HEAVEN which is composed of three stacked yang (+) Lines.  The crucial idea here is that the identity element differs for each dimensional context,  and whatever that context might be,  it produces no change when in the operation of multiplication it acts as operator on any operand within the stated dimension.^[3]

As a corollary it can be stated that any number in any dimension n composed of  any combination  of  yang Lines (+1) and yin Lines (-1) if multiplied by itself (i.e., squared) produces the identity element for that dimension.  In concrete terms this means, for example, that any bigram multiplied by itself equals the bigram OLD YANG; any of eight trigrams multiplied by itself  equals the trigram HEAVEN;  and  any of the sixty-four hexagrams multiplied by itself  equals the hexagram HEAVEN; etc. (valid for any and all dimensions without exception). Consequently, the number of roots the identity element has in any dimension n is equal to the number 2ⁿ, these all being real roots in that particular dimension.

Similar contextual analysis would show that the inversion element of any dimension n  has  2ⁿ roots of the kind we have agreed to refer to as contra-square roots in deference to the Mathematics Establishment.^[4]

That leads us to the possibly startling conclusion that in every dimension n  there is an  inversion element  that has the same number of roots as the identity elementandall of them are real roots.  For two dimensions the two pairs that satisfy the requirement are bigram pairs

For one dimension there is only a single pair that satisfies. That is (surprise, surprise)  yin(-1)/yang (+1).  What it comes down to is
this:

If we are going to continue to insist on referring to square root
in terms of the one-dimensional number line, then

• +1 has two real roots of the traditional variety, +1 and -1
• -1 has two real roots of the newly defined contra variety,
  +1/-1 and -1/+1

So where do imaginary numbers and quaternions fit in all this? The short answer is they don’t.  Imaginary numbers entered the annals of human thought through error.  There was a pivotal moment^[5]  in the history of mathematics and science, an opportunity to see that there are in every dimension two different kinds of roots - - - what has been called square root and what we are calling contra-square roots.  Enlightenment mathematicians and philosophers  essentially allowed the opportunity to slip through their fingers unnoticed.^[6]

Descartes at least saw through the veil.  He called the whole matter of imaginary numbers ‘preposterous’.  It seems his venerable opinion was overruled though. Isaac Newton had his say in the matter too. He claimed that roots of imaginary numbers “had to occur in pairs.” And yet another great mathematician, philosopher opined.  Gottfried Wilhelm Leibniz,  in 1702 characterized √−1 as  “that amphibian between being and non-being which we call the imaginary root of negative unity.” Had he but preserved such augury conspicuously in mind he might have elaborated the concept of probable numbers in the 18th century.  If only he had truly understood the I Ching,  instead of dismissing it as a primitive articulation of his own binary number system.

(continuedhere)

Image: The four quadrants of the Cartesian plane. By convention the quadrants are numbered in a counterclockwise direction.  It is as though two number lines were placed together, one going left-right, and the other going up-down to provide context for the two-dimensional plane. Sourced from Math Is Fun.

Notes

[1] My preference might be for square root to be redefined from the bottom up, but I don’t see that happening in our lifetimes. Then too this way could be better.

[2] By the term unit number,  I intend any number of a given dimension that consists entirely of variant elements of the number one (1) in either its positive or negative manifestation.  Stated differently,  these are vectors having various different directions within the dimension,  but all of scalar value -1 (yin) or +1 (yang). All emblems of I Ching symbolic logic satisfy this requirement. These include the Line, bigram, trigram, tetragram, and hexagram.  In any dimension n there exist 2ⁿ such emblems.  In sum, for our purposes here, a unit number is any of the set of numbers, within any dimension n, which when self-multiplied (squared) produces the multiplicative identity of that dimension which is itself, of course, a member of the set.

ADDENDUM (01 MAY 2016): I’ve since learned that mathematics has a much simpler way of describing this. It calls all these unit vectors. Simple, yes?

[3] I think it fair to presume that this might well have physical correlates in terms of quantum mechanical states or numbers. Here’s a thought: why would it be necessary that all subatomic particles exist in the same dimension at all times given that they have a playing field of multiple dimensions, - some of them near certainly beyond the three with which we are familiar? And why would it not be possible for two different particles to be stable and unchanging in their different dimensions,  yet become reactive and interact with one another when both enter the same dimension or same amplitude of dimension?

[4] Since in any contra-pair (antipodal opposites) of any dimension, either member of the pair must be regarded  once as operator  and  once as operand. So for the two-dimensional square, for example, there are two antipodal pairs (diagonals) and either vertex of each can be either operator or operand.  So in this case, 2 x 2 = 4.  For trigrams there are four antipodal pairs, and 2 x 4 = 8. For hexagrams there are thirty-two antipodal pairs and 2 x 32 = 64. In general, for any dimension n there are 2 x 2ⁿ/2 = 2ⁿ antipodal pairs or contra-roots.

[5] Actually lasting several centuries, from about the 16th to the 19th century. Long enough,  assuredly,  for the error  to have been  discovered and corrected. Instead,  the 20th century dawned with error still in place,  and physicists eager to explain the newly discovered bewildering quantum phenomena compounded the error  by latching onto  √−1 and quaternions  to assuage their confusion and discomfiture.  This probably took place in the early days of quantum mechanics when the Bohr model of the atom still featured electrons as traveling in circular orbits around the nucleus or soon thereafter, visions of minuscule solar systems still fresh in the mind. At that time rotations detailed by imaginary numbers and quaternions may have still made some sense. Such are the vagaries of history.

[6] I think an important point to consider is that imaginary and complex numbers were, -to mathematicians and physicists alike,- new toys of a sort that  enabled them  to  accomplish certain things  they could not otherwise. They were basically tools of empowerment which allowed manipulation of numbers and points on a graph more easily or conveniently.  They provided
their controllers a longed for power over symbols, if not over the real world itself. In the modern world ever more of what we humans do and want to do involves manipulation of symbols. Herein,  I think,  lies the rationale for our continued fascination with and dependence on these tools of the trade. They don’t need to actually apply to the world of nature,  the noumenal world,  so long as they satisfy human desire for domination  over the world of symbols it has created for itself and in which it increasingly dwells, to a considerable degree apart from the natural world’s sometimes seemingly too harsh laws.

© 2016 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 310-

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - IV

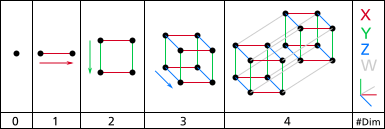
(continued from here)

One of the notable things the Rationalists  failed to take into account in their analysis and codification of square roots  was  the significance of context. In so doing they assured that all related concepts they developed would eventually degenerate into a series of errors of conflation.  Do  not ever underestimate the importance of context.

Mathematicians, for example, can show that for any 3-dimensional cube  there exists  a  2-dimensional square,  the area of which equals the volume of the cube.^[1] And although that is true, something has been lost in translation. This is another of the sleights of hand mathematicians are so fond of.  Physicists cannot afford to participate in such parlor tricks as these, however mathematically true they might be.^[2]

We will begin now, then, to examine how the mandalic coordinate approach stacks up against that of imaginary numbers and quaternions. The former are holistic and respective of the natural order; the latter are irresponsibly rational, simplistic and, in final analysis, wrong about how nature works.^[3] Ambitious endeavor indeed, but let’s give it a go.

We’ve already looked at how the standard geometric interpretation of imaginary numbers in context of the complex plane is based on rotations through continuous Euclidean space.  You can brush up on that aspect of the story here if necessary. The mandalic approach to mapping of space is more complicated and far more interesting.  It involves multidimensional placement of elements in a discrete space, which is to say a discontinuous space,  but one fully commensurate with both Euclidean and Cartesian 3-dimensional space. The holo-interactive manner in which these elements relate to one another leads to a  probabilistic mathematical design  which preserves commutative multiplication,  unlike quaternions which forsake it.

Transformations between these elements are based on inversion (reflection through a point) rather than rotation which cannot in any case reasonably apply to discrete spaces.  The spaces that quantum mechanics inhabits are decidedly discrete.  They cannot be accurately detailed using imaginary and complex numbers or quaternions.  To discern the various, myriad transitions which can occur among mandalic coordinates requires some patience. I think it cannot be accomplished overnight but at least in the post next up we can make a start.^[4]

(continuedhere)

Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions  (A tesseract).  There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

Notes

[1] If only in terms of scalar magnitude. Lost in translation are all the details relating to vectors and dimensions in the original.  Conflation does not itself in every case involve what might be termed ‘error’ but because it always involves loss or distortion of information,  it is nearly always guaranteed to eventuate in error somewhere down the line of argument. The point of all this in our context here is that, in the history of mathematics, something of this sort occurred when the Rationalists of the Enlightenment invented imaginary and complex numbers and again when quaternions were invented in 1843. These involved a disruption of vectors and dimensions as treated by nature. The loss of information involved goes a long way in explaining why no one has been able to explain whyandhow quantum mechanics works in a century or more.  These  misconstrued theses  of mathematics behave like a demon or ghost in the machine that misdirects,  albeit unintentionally, all related thought processes.  What we end up with is a plethora of confusion. The fault is not in quantum mechanics but in ourselves, that we are such unrelentingly rational creatures, that so persistently pursue an unsound path that leads to reiterative error.

[2] Because physicists actually care about the real world; mathematicians, not so much.

[3] It must be admitted though that it was not the mathematicians who ever claimed imaginary numbers had anything to do with nature and the real world. Why would they? Reality is not their concern or interest. No, it was physicists themselves who made the mistake. The lesson to be learned by physicists here I expect is to be careful whose petticoat they latch onto. Not all are fabricated substantially enough to sustain their thoughts about reality, though deceptively appearing to do just that for protracted periods of time.

[4] My apologies for not continuing with this here as originally intended. To do so would make this post too long and complicated. Not that transformations among mandalic coordinates are difficult to understand,  just that they are very convoluted. This is not a one-point-encodes-one-resident-number plan like that of Descartes we’re talking about here. This is mandala country.

© 2016 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 309-

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - III

(continued from here)

My objection to the imaginary dimension is not that we cannot see it.  Our senses cannot identify probable dimensions either, at least not in the visually compelling manner they can the three Cartesian dimensions. The question here is not whether imaginary numbers are mathematically true. How could they not be? The cards were stacked in their favor. They were defined in such a manner, – consistently and based on axioms long accepted valid, – that they are necessarily mathematically true. There’s a word for that sort of thing. –The word is  tautological.– No,  the decisive question is whether imaginary numbers apply to the real world; whether they are scientifically true, and whether physicists can truly rely on them to give empirically verifiable results with maps that accurately reproduce mechanisms actually used in nature.^[1]

The geometric interpretation of imaginary numbers was established as a belief system using the Cartesian line extending from  -1,0,0  through the origin  0,0,0 to 1,0,0  as the sole real axis left standing in the complex plane. In 1843,  William Rowan Hamilton introduced two additional axes in a quaternion coordinate system.  The new jandk axes,  similar to the i axis, encode coordinates of imaginary dimensions.  So the complex plane has one real axis, one imaginary; the quaternion system, three imaginary axes, one real, to accomplish which though involved loss of commutative multiplication. The mandalic coordinate system has three real axes upon which are superimposed six probable axes. It is both fully commensurate with the Cartesian system of real numbers  and  fully commutative for all operations throughout all dimensions as well.^[2]

All of these coordinate systems have a central origin point which all other points use as a locus of reference to allow clarity and consistency in determination of location.  The  mandalic coordinate system  is unique in that this point of origin is not a  null point of emptiness as in all the other locative systems,  but  a point of effulgence.  In that location  where occur Descartes’ triple zero triad (0.0.0) and the complex plane’s real zero plus imaginary zero (ax=0,bi=0), we find eight related hexagrams, all having neutral charge density,  each of these consisting of  inverse trigrams  with corresponding Lines of opposite charge, canceling one another out. These eight hexagrams are the only hexagrams out of sixty-four total possessing both of these characteristics.^[3]

So let’s begin now to plot the points of the mandalic coordinate system with  the view  of comparing its  dimensions and points  with  those of the complex plane.^[4]  The eight  centrally located hexagrams  all refer to  and are commensurate with the Cartesian triad (0,0,0). In a sense they can be considered eight  alternative possible states  which can  exist in this locale at different times. These are hybrid forms of the four complementary pair of hexagrams found at antipodal vertices of the mandalic cube.  The eight vertex hexagrams are those with upper and lower trigrams identical. This can occur nowhere else in the mandalic cube because there are only eight trigrams.^[5]

From the origin multiple probability waves of dimension radiate out toward the  central points of the faces of the cube,  where these divergent force fields rendezvous and interact with reciprocal forces returning from the eight vertices at the periphery. converging toward the origin.  Each of these points at the six face centers  are  common intersections  of another eight particulate states or force fields analogous to the origin point except that four originate within this basic mandalic module and four without in an adjacent tangential module. Each of the six face centers then is host to four internal resident hexagrams which  share the point in some manner, time-sharing or other. The end result is the same regardless, probabilistic expression of  characteristic form and function.  There is a possibility that this distribution of points and vectors  could be or give rise to a geometric interpretation of the Schrödinger equation,  the fundamental equation of physics for describing quantum mechanical behavior. Okay, that’s clearly a wild claim, but in the event you were dozing off you should now be fully awake and paying attention.

The vectors connecting centers of opposite faces of an ordinary cube through the cube center or origin of the Cartesian coordinate system are at 180° to each other forming the three axes of the system corresponding to the number of dimensions.  The mandalic cube has 24 such axes, eight of which accompany each Cartesian axis thereby shaping a hybrid 6D/3D coordinate system. Each face center then hosts internally four hexagrams formed by  hybridization of trigrams  in  opposite vertices  of diagonals of that cube face,  taking one trigram  (upper or lower)  from one vertex and the other trigram (lower or upper) from the other vertex. This means that a face of the mandalic cube has eight diagonals, all intersecting at the face center, whereas a face of the ordinary cube has only two.^[6]

The circle in the center of this figure is intended to indicate that the two pairs of antipodal hexagrams at this central point of the cube face rotate through 90° four times consecutively to complete a 360° revolution. But I am describing the situation here in terms of revolution only to show an analogy to imaginary numbers.  The actual mechanisms involved can be better characterized as inversions (reflections through a point),  and the bottom line here is that for each diagonal of a square, the corresponding mandalic square has  a possibility of 4 diagonals;  for each diagonal of a cube,  the corresponding mandalic cube has a possibility of 8 diagonals. For computer science, such a multiplicity of possibilities offers a greater number of logic gates in the same computing space and the prospect of achieving quantum computing sooner than would be otherwise likely.^[7]

Similarly, the twelve edge centers of the ordinary cube host a single Cartesian point,  but the superposed mandalic cube hosts two hexagrams at the same point. These two hexagrams are always inverse hybrids of the two vertex hexagrams of the particular edge.  For example,  the edge with vertices  WIND over WIND  and  HEAVEN over HEAVEN  has as the two hybrid hexagrams  at the  center point  of the edge  WIND over HEAVEN  and HEAVEN over WIND. Since the two vertices of concern here connect with one another  via  the horizontal x-dimension,  the two hybrids  differ from the parents and one another only in Lines 1 and 4 which correspond to this dimension.  The other four Lines encode the y- amd z-dimensions, therefore remain unchanged during all transformations undergone in the case illustrated here.^[8]

This post began as a description of the structure of the mandalic coordinate system and how it differs from those of the complex plane and quaternions.  In the composition,  it became also  a passable introduction to the method of  composite dimension.  Additional references to the way composite dimension works  can be found scattered throughout this blog and Hexagramium Organum.  Basically the resulting construction can be thought of as a  tensegrity structure,  the integrity of which is maintained by opposing forces in equilibrium throughout, which operate continually and never fail,  a feat only nature is capable of.  We are though permitted to map the process  if we can manage to get past our obsession with  and addiction to the imaginary and complex numbers and quaternions.^[9]

In our next session we’ll flesh out probable dimension a bit more with some illustrative examples. And possibly try putting some lipstick on that PIG (Presumably Imaginary Garbage) to see if it helps any.

(continuedhere)

Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions  (A tesseract).  There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

Notes

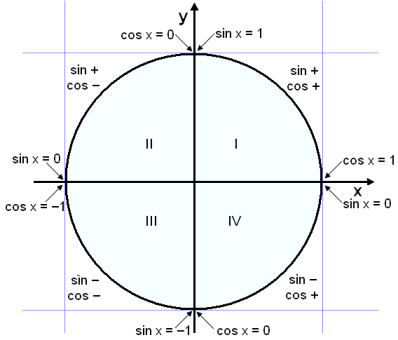
[1] For more on this theme,  regarding quaternions,  see Footnote [1]  here. My own view is that imaginary numbers, complex plane and quaternions are artificial devices, invented by rational man, and not found in nature.  Though having limited practical use in  representation of rotations  in  ordinary space they have no legitimate application to quantum spaces,  nor do they have any substantive or requisite relation to square root, beyond their fortuitous origin in the Rationalists’ dissection and codification of square root historically, but that part of the saga was thoroughly misguided.   We wuz bamboozled.  Why persist in this folly? Look carefully without preconception and you’ll see this emperor’s finery is wanting. It is not imperative to use imaginary numbers to represent rotation in a plane. There are other, better ways to achieve the same. One would be to use sin and cos functions of trigonometry which periodically repeat every 360°.  (Read more about trigonometric functions here.)  Another approach would be to use polar coordinates.

[SOURCE]

A quaternion, on the other hand,  is a four-element vector composed of a single real element and three complex elements. It can be used to encode any rotation in a  3D coordinate system.  There are other ways to accomplish the same, but the quaternion approach offers some advantages over these.  For our purposes here what needs to be understood is that mandalic coordinates encode a hybrid 6D/3D discretized space. Quaternions are applicable only to continuous three-dimensional space.  Ultimately,  the two reside in different worlds and can’t be validly compared. The important point here is that each has its own appropriate domain of judicious application. Quaternions can be usefully and appropriately applied to rotations in ordinary three-dimensional space, but not to locations or changes of location in quantum space.  For description of such discrete spaces, mandalic coordinates are more appropriate, and their mechanism of action isn’t rotation but inversion (reflection through a point.) Only we’re not speaking here about inversion in Euclidean space, which is continuous, but in discrete space, a kind of quasi-Boolean space,  a higher-dimensional digital space  (grid or lattice space). In the case of an electron this would involve an instantaneous jump from one electron orbital to another.

[2] I think another laudatory feature of mandalic coordinates is the fact that they are based on a thought system that originated in human prehistory, the logic of the primal I Ching. The earliest strata of this monumental work are actually a compendium of combinatorics and a treatise on transformations,  unrivaled until modern times, one of the greatest intellectual achievements of humankind of any Age.  Yet its true significance is overlooked by most scholars, sinologists among them.  One of the very few intellectuals in the West who knew its true worth and spoke openly to the fact, likely at no small risk to his professional standing, was Carl Jung, the great 20th century psychologist and philosopher.

It is of relevance to note here that all the coordinate systems mentioned are, significantly,  belief systems of a sort.  The mandalic coordinate system  goes beyond the others though,  in that it is based on a still more extensive thought system, as the primal I Ching encompasses an entire cultural worldview.  The question of which,  if any,  of these coordinate systems actually applies to the natural order is one for science, particularly physics and chemistry, to resolve.

Meanwhile, it should be noted that neither the complex plane nor quaternions refer to any dimensions beyond the ordinary three, at least not in the manner of their current common usage.  They are simply alternative ways of viewing and manipulating the two- and three-dimensions described by Euclid and Descartes. In this sense they are little different from  polar coordinatesortrigonometry  in what they are attempting to depict.  Yes, quaternions apply to three dimensions, while polar coordinates and trigonometry deal with only two.  But then there is the method of  Euler angles  which describes orientation of a rigid body in three dimensions and can substitute for quaternions in practical applications.

A mandalic coordinate system, on the other hand, uniquely introduces entirely new features in its composite potential dimensions and probable numbers which I think have not been encountered heretofore. These innovations do in fact bring with them  true extra dimensions beyond the customary three  and also the novel concept of dimensional amplitudes.  Of additional importance is the fact that the mandalic method relates not to rotation of rigid bodies,  but to interchangeability and holomalleability of parts  by means of inversions through all the dimensions encompassed, a feature likely to make it useful for explorations and descriptions of particle interactions of quantum mechanics.  Because the six extra dimensions of mandalic geometry may, in some manner, relate to the six extra dimensions of the 6-dimensional Calabi–Yau manifold, mandalic geometry might equally be of value in string theoryandsuperstring theory.

Itis possible to use mandalic coordinates to describe rotations of rigid bodies in three dimensions,  certainly,  as inversions can mimic rotations, but this is not their most appropriate usage. It is overkill of a sort. They are capable of so much more and this particular use is a degenerate one in the larger scheme of things.

[3] This can be likened to a quark/gluon soup.  It is a unique and very special state of affairs that occurs here. Physicists take note. Don’t let any small-minded pure mathematicians  dissuade you from the truth.  They will likely write all this off as “sacred geometry.” Which it is, of course, but also much more.  Hexagram superpositions  and  stepwise dimensional transitions  of the mandalic coordinate system could hold critical clues  to  quantum entanglement and quantum gravity. My apologies to those mathematicians able to see beyond the tip of their noses. I was not at all referring to you here.

[4] Hopefully also with dimensions and points of the quaternion coordinate system once I understand the concepts involved better than I do currently. It should meanwhile be underscored that full comprehension of quaternions is not required to be able to identify some of their more glaring inadequacies.

[5] In speaking of  "existing at the same locale at different times"  I need to remind the reader and myself as well that we are talking here about  particles or other subatomic entities that are moving at or near the speed of light,- - -so very fast indeed. If we possessed an instrument that allowed us direct observation of these events,  our biologic visual equipment  would not permit us to distinguish the various changes taking place. Remember that thirty frames a second of film produces  the illusion of motion.  Now consider what  thirty thousand frames  a second  of  repetitive action  would do.  I think it would produce  the illusion of continuity or standing still with no changes apparent to our antediluvian senses.

[6] Each antipodal pair has four different possible ways of traversing the face center.  Similarly,  the mandalic cube has  thirty-two diagonals  because there are eight alternative paths by which an antipodal pair might traverse the cube center. This just begins to hint at the tremendous number of  transformational paths  the mandalic cube is able to represent, and it also explains why I refer to dimensions involved as  potentialorprobable dimensions  and planes so formed as probable planes.  All of this is related to quantum field theory (QFT), but that is a topic of considerable complexity which we will reserve for another day.

[7] One advantageous way of looking at this is to see that the probabilistic nature of the mandalic coordinate system in a sense exchanges bits for qubits and super-qubits through creation of different levels of logic gates that I have referred to elsewhere as different amplitudes of dimension.

[8] Recall that the Lines of a hexagram are numbered 1 to 6, bottom to top. Lines 1 and 4 correspond to, and together encode, the Cartesian x-dimension. When both are yang (+),  application of the method of  composite dimension results in the Cartesian value  +1;  when both yin (-),  the Cartesian value  -1. When either Line 1 or Line 4 is yang (+) but not both (Boole’s exclusive OR) the result is one of two possible  zero formations  by destructive interference. Both of these correspond to (and either encodes) the single Cartesian zero (0). Similarly hexagram Lines 2 and 5 correspond to and encode the Cartesian y-dimension; Lines 3 ane 6, the Cartesian z-dimension. This outline includes all 9 dimensions of the hybrid  6D/3D coordinate system:  3 real dimensions and the 6 corresponding probable dimensions. No imaginary dimensions are used; no complex plane; no quaternions. And no rotations. This coordinate system is based entirely on inversion (reflection through a point)  and on constructive or destructive interference. Those are the two principal mechanisms of composite dimension.

[9] The process as mapped here is an ideal one.  In the real world errors do occur from time to time. Such errors are an essential and necessary aspect of evolutionary process. Without error, no change. And by implication, likely no continuity for long either, due to external damaging and incapacitating factors that a natural world devoid of error never learned to overcome.  Errors are the stepping stones of evolution, of both biological and physical varieties.

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - II

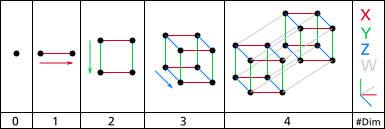
(continued from here)

When a geometric interpretation of imaginary numbers was at last proposed,  long after they were invented,  it was as though accomplished by central committee. The upshot was easily enough understood but also simplistic. In broad brushstroke here is what seems to have gone down.

The 3 dimensions of Descartes’ coordinate system-a number already deficient from the perspective of mandalic geometry-were reduced to just one.  Of the real number axes then  only the x-axis remained.  This meant from the get-go  that  any  geometric figure that ensued  could encompass only linearity in terms of real numbers and dimensions.  It was applicable only to a line segment,  so the complex plane that resulted  could describe just one real dimension and one imaginary dimension.  It consecrated the number line in a single dimension, to exclusion of its proper habitation in two others besides. Strike one for imaginary numbers.^[1]

With that as background let’s look now at the rotations described by this geometric interpretation of imaginary numbers in the context of the complex plane.

i in the complex or cartesian plane. Real numbers lie on the horizontal axis, and imaginary numbers lie on the vertical axis By Loadmaster (David R. Tribble) (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

The number 1 is the multiplicative identity element for real numbers and the number -1  is the  reflection inversion element  for real numbers.  Put another way, the number one times any number equals that number;  the number -1 times any number is  a negative of that number  or  the inverse number through a reference point, usually taken as zero. Multiplying by 1 then leaves 1, -1, i and -i all unchanged. Multiplying by -1  changes  -1 to 1, 1 to -1, i to -i, and -i to i.  In terms of rotations in the complex plane, these changes  all involve a rotation through 180 degrees.  Multiplication of the number 1 by i changes it to i; i by i changes it to -1; -1 by i to -i; and -i by i to 1.  These changes all involve rotations through 90 degrees.  And finally, multiplication of 1 by -i changes it to -i; -i by -i changes it to -1; -1 by -i to i; and i by -i to 1: all changes involving rotations through -90 degrees.

The figure below shows another way to interpret these rotations that amounts to the same tbing: i¹ = i; i² =-1; i³ = -i; i⁴ = 1.  Click to enlarge.

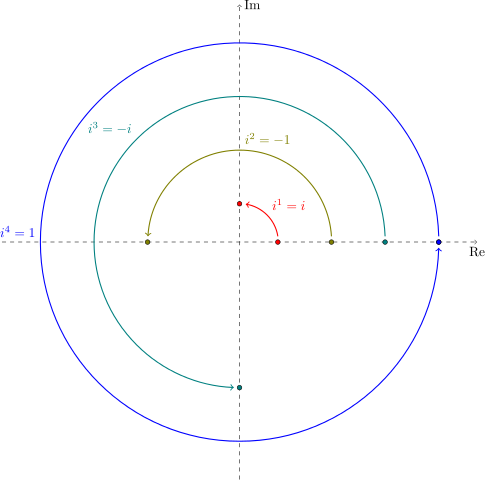
Four numbers on the real line multiplied by integer powers of the imaginary unit, which corresponds to rotations by multiples of the right angle. By Keφr [CC0],via Wikimedia Commons

I think a committee of some sort must have come up with this resplendent plan. For certain it was an Academy of Mathematics and Sciences that endorsed and enthroned it. All bow to central authority.

I had planned to include a comparison of imaginary numbers and probable numbers in this post as well but because that is a long discussion itself, it will have to wait till the next post.  I might add it should prove well worth the wait.

(continuedhere)

Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions  (A tesseract).  There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

Notes

[1] Mathematician William Rowan Hamilton  subsequently addressed this deficiency in 1843 with his  quaternions,  a  number system  that  extends the complex numbers to three-dimensional space.  Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space  or,  in other words, as the quotient of two vectors.  This complicated matters even more by introducing a non-commutative multiplication operation to the system, though to be fair the quaternion coordinate system has found some useful applications mainly for calculations involving 3-dimensional rotations,  as in 3-dimensional computer graphics,computer vision, and crystallographic texture analysis. Still it becomes problematic when theoretical physics attempts use of quaternions in calculations pertaining to  atomic and subatomic spaces  where rotations do not actually take place.  The conclusion to be drawn here is that quaternions can be usefully,  if somewhat clumsily,  applied to 3-dimensional macro-spaces but are inapproriate for accurate description of higher dimensional spaces. What is here unfortunate and misleading  is that quaternions apparently do describe outcomes of events in the quantum realm to some partial degree,  if not the mechanisms of the events themselves.  Physicists would not long tolerate them were that not so.

[ADDENDUM (24 APRIL, 2016)
Since writing this I’ve learned that quaternions are not currently used in quantum physics nor were they ever, to any great degree, in the past.]

In other words, sometimes  the right answer  can be reached by a wrong method. In the case under discussion here, we should note that it is possible for a rotation to mimic inversion (reflection through a point). A 90° rotation in two dimensions can mimic a single inversion in a single plane through an edge of a square, and a 180° rotation in two dimensions can mimic a single inversion through a diagonal of a square  or  two successive inversions  through  two perpendicular edges of a square.  A 180° rotation in three dimensions  can mimic three inversions through three mutually perpendicular edges of a square;  a combination of  one inversion through a diagonal of a square  and another through an edge perpendicular to the plane of the first inversion;  or a single inversion through a diagonal of the cube. Subatomic paricles exist as discrete or quantized entities and would follow such methods of transformation rather than rotations through a continuous space.  Of course, transformations involving a diagonal would require more transformative energy than one involving a single edge.

Such patterns of relationship and transformation could no doubt be described in terms of quantum states and quantum numbers without too much difficulty by a knowledgeable theoretical physicist.  Surely doing so could be no more difficult than using quaternions,  which may give a correct answer while also misleading and limiting knowledge of the the true workings of the quantum realm by using an incorrect mechanism, one non-commutative to boot. Nature doesn’t approve of hat tricks like that.

Beyond Descartes - Part 9:
The Potential Plane
and Probable States of Change

Composite Dimension and
Amplitudes of Potentiality
Episode 3

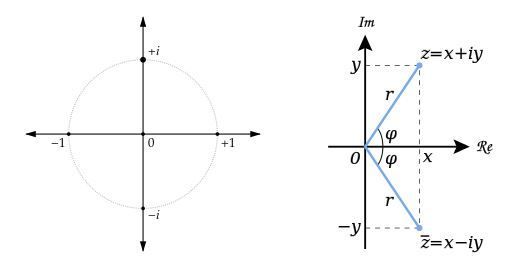
(continued from here)

We have seen that an imaginary number is a complex number that can be written as a real number multiplied by the imaginary unit i,  which is defined by its property ixi =−1.  The square of an imaginary number bi is −b².  For example,  6i is an imaginary number,  and its square is −36.^[1] Other than 0,  imaginary numbers yield negative real numbers when they are squared.^[2]

Turning now to potential numbers, we can similarly define a unit of potentiality p by the property p x -p = -1. [Long pause here waiting for the other shoe to drop.] Just a minute, you say, that’s just like 1 x -1 = -1.  Yes, it is. And that is just the point. All real numbers. Nothing to imagine. And Descartes finally vindicated after all these years - imaginary numbers just imaginary after all.  But how does this work? Or does it even work?  What exactly is the point? Is this a joke? It’s no joke, I assure you.  It’s an easier and better way to achieve the same ends - - - and more. Muchmore.

The secret is in the sauce, I say slyly. Really? Well, yes - in a way. Though imaginaries use a sauce with nearly identical ingredients.  The recipe is p + (-p) = 0. And, of course, i + (-i) = 0 as well.  The trick is in how - - - and where - - - the sauce is applied.  In the potential plane the sauce is applied more liberally in more locations for greater lubrication.

Levity aside. (This is after all a TST^[3].) The complex plane uses a single axis.  This axis represents a new dimension, wholly distinct from the x, y and z dimensions.  Strangely,  we’re never informed where this axis/dimension might be located,  just that it is somewhere other than where x, y and z are located. Stranger still, the complex plane allocates the y-axis of the Cartesian plane for its own use in location of its points. Although never specifically mentioned, to my knowledge, I surmise the imaginary dimension exists in what mathematics and physics both call phase space.^[4]

The mandalic or potential plane uses no such underhanded plan. It openly posits the existence of six new dimensions, allocated equally with two accompanying each of the Cartesian dimensions,  all overtly evident. (All nine spatial dimensions in plain sight together, that is.)  Nothing left to the imagination. As the new dimensions are made commensurate with the old in a hybrid geometric display,  no imaginary dimension is needed. Coordinates of  all potential dimensions  are  readily communicable  with the real number system through all of the ordinary Cartesian dimensions concurrently along with the Cartesian coordinates.  Moreover,  mandalic geometry conjectures that the ordinary Cartesian dimensions may in fact originate in  interactions among number species  of potential dimensions filtered through impacts on inherited biological sensory mechanisms.^[5] This raises yet another interesting possibility.^[6]

In the long convoluted history of mathematics, the imaginary numbers were introduced as a correlative to the number line with its real numbers. That meant, among other things, that they were linear, consisting of a single dimension.  The  complex plane  related the two
in a kind of hybrid geometry that consisted of one real dimension and one imaginary dimension.  Mathematician  William Rowan Hamilton in 1843 proffered the  quaternions,  a number system that extends the complex numbers to three dimensions, whereupon things went, to my mind, from bad, to very much worse.

Quaternions came with certain dysfunctional characteristics, among them,  the fact that multiplication of two quaternions is noncommutative. This is problematic.  The imaginary and complex numbers,  at least,  had both been commutative.  Nevertheless, physics endorsed the quaternions as it earlier had imaginary and complex numbers.

Why? Because the quaternions do in fact give partly correct results, and when investigating a dimly illuminated region of reality, such as the subatomic world still is today, even partial results are heartily welcomed if that is all that can be had.  The sad consequence of this, is that physics has been led astray in its quest for truth for over a century now,  because partial truths can be much more misleading than complete errors. Total error is often uncovered much sooner than partial truth, which can pass undiscovered, depending upon circumstances, for a very long time.

Mandalic geometry will be shown to be free of the difficulty posed by noncommutative multiplication. It is fully commutative throughout its nine dimensions (three ordinary, six extraordinary). It was not composed that way from a number line,  with elements that could be commutatively multiplied with one another. It came that way fully formed from the start, in its primeval embodiment  as a multidimensional structure,  expressing behavior intrinsic to holistic nature.

Next time around, we’ll begin to look under the hood of the mandalic approach to geometry and see if we can grokit.

(continuedhere)

Image: (lower left) Imaginary unit i in the complex or Cartesian plane. Real numbers lie on horizontal axis, imaginary numbers on the vertical axis.  By Loadmaster  (David R. Tribble), (Own work) [CC BY-SA 3.0orGFDL], via Wikimedia Commons; (lower right) A diagram of the complex plane. The imaginary numbers are on the vertical axis, the real numbers on the horizontal axis. By Oleg Alexandrov [GFDLorCC-BY-SA-3.0],via Wikimedia Commons

Notes

[1] 6²xi² = 36 x (-1) = -36.

[2] Zero (0) is considered both real and imaginary, and both the real part and the imaginary part are defined as real numbers. (If that makes little sense to you, don’t blame me. I’m just the messenger here, reporting what the mathematicians have stated to be the case.) This seems to me to be purely an arbitrary definition, and it confuses me as much as it probably does you.  Could it be they did this to avoid the situation where 0² x (-1) = -0?  I think I would find that definition less disturbing, welcome even.

[3] Newly coined Internet acronym for Truly Serious Topic. (Not to be confused with TSR Totally Stupid Rules.)

Speaking about “greater lubrication”(wewere a moment ago, remember?), I use the phrase not simply as  a figure of speech,  or a simile,  but rather,  as a metaphor.  "Spicing" of mandalic geometry with all those zeros of potentiality makes for a very “fluidic dish” which, I believe, reflects the changeable nature of reality far better than the stricter, strait-laced coordinates of Descartes or the complex plane are able to do. And it’s not just a matter of fluidity involved here. The mandalic form so begotten is, in fact, a probability distribution through the three Cartesian dimensions concurrently,  which feature alone  makes mandalic geometry an ideal candidate for application to quantum physics.

[4] A phase space of a dynamical system is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space. In a phase space every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane.  For every possible state of the system (that is to say, any allowed combination of values of the system’s parameters) a point is included in the multidimensional space. [Wikipedia]

[5] I am speaking here of the hybrid 6D/3D formulation of mandalic geometry which combines the features of  dimensional numbers,  potential numbers,  and composite dimension,  this being a fully open access geometric system that has nothing hidden, nothing held back. What you see is what you get. (WYSIWYG)

[6] It is tempting to wonder whether there might be a close connection between the composite dimensions/potential coordinates  proposed by mandalic geometry and the pilot wave theoryorde Broglie–Bohm theory of quantum mechanics. At least there seems to be a correlation  between  David Bohm’s implicate/explicate order and the manifest/unmanifest (potential) coordinates of mandalic geometry.

© 2015 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 285-

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - III

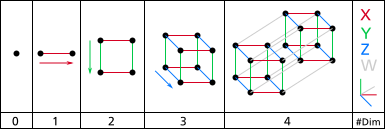
(continued from here)

My objection to the imaginary dimension is not that we cannot see it.  Our senses cannot identify probable dimensions either, at least not in the visually compelling manner they can the three Cartesian dimensions. The question here is not whether imaginary numbers are mathematically true. How could they not be? The cards were stacked in their favor. They were defined in such a manner, – consistently and based on axioms long accepted valid, – that they are necessarily mathematically true. There’s a word for that sort of thing. –The word is  tautological.– No,  the decisive question is whether imaginary numbers apply to the real world; whether they are scientifically true, and whether physicists can truly rely on them to give empirically verifiable results with maps that accurately reproduce mechanisms actually used in nature.^[1]

The geometric interpretation of imaginary numbers was established as a belief system using the Cartesian line extending from  -1,0,0  through the origin  0,0,0 to 1,0,0  as the sole real axis left standing in the complex plane. In 1843,  William Rowan Hamilton introduced two additional axes in a quaternion coordinate system.  The new jandk axes,  similar to the i axis, encode coordinates of imaginary dimensions.  So the complex plane has one real axis, one imaginary; the quaternion system, three imaginary axes, one real, to accomplish which though involved loss of commutative multiplication. The mandalic coordinate system has three real axes upon which are superimposed six probable axes. It is both fully commensurate with the Cartesian system of real numbers  and  fully commutative for all operations throughout all dimensions as well.^[2]

All of these coordinate systems have a central origin point which all other points use as a locus of reference to allow clarity and consistency in determination of location.  The  mandalic coordinate system  is unique in that this point of origin is not a  null point of emptiness as in all the other locative systems,  but  a point of effulgence.  In that location  where occur Descartes’ triple zero triad (0.0.0) and the complex plane’s real zero plus imaginary zero (ax=0,bi=0), we find eight related hexagrams, all having neutral charge density,  each of these consisting of  inverse trigrams  with corresponding Lines of opposite charge, canceling one another out. These eight hexagrams are the only hexagrams out of sixty-four total possessing both of these characteristics.^[3]

So let’s begin now to plot the points of the mandalic coordinate system with  the view  of comparing its  dimensions and points  with  those of the complex plane.^[4]  The eight  centrally located hexagrams  all refer to  and are commensurate with the Cartesian triad (0,0,0). In a sense they can be considered eight  alternative possible states  which can  exist in this locale at different times. These are hybrid forms of the four complementary pair of hexagrams found at antipodal vertices of the mandalic cube.  The eight vertex hexagrams are those with upper and lower trigrams identical. This can occur nowhere else in the mandalic cube because there are only eight trigrams.^[5]

From the origin multiple probability waves of dimension radiate out toward the  central points of the faces of the cube,  where these divergent force fields rendezvous and interact with reciprocal forces returning from the eight vertices at the periphery. converging toward the origin.  Each of these points at the six face centers  are  common intersections  of another eight particulate states or force fields analogous to the origin point except that four originate within this basic mandalic module and four without in an adjacent tangential module. Each of the six face centers then is host to four internal resident hexagrams which  share the point in some manner, time-sharing or other. The end result is the same regardless, probabilistic expression of  characteristic form and function.  There is a possibility that this distribution of points and vectors  could be or give rise to a geometric interpretation of the Schrödinger equation,  the fundamental equation of physics for describing quantum mechanical behavior. Okay, that’s clearly a wild claim, but in the event you were dozing off you should now be fully awake and paying attention.

The vectors connecting centers of opposite faces of an ordinary cube through the cube center or origin of the Cartesian coordinate system are at 180° to each other forming the three axes of the system corresponding to the number of dimensions.  The mandalic cube has 24 such axes, eight of which accompany each Cartesian axis thereby shaping a hybrid 6D/3D coordinate system. Each face center then hosts internally four hexagrams formed by  hybridization of trigrams  in  opposite vertices  of diagonals of that cube face,  taking one trigram  (upper or lower)  from one vertex and the other trigram (lower or upper) from the other vertex. This means that a face of the mandalic cube has eight diagonals, all intersecting at the face center, whereas a face of the ordinary cube has only two.^[6]

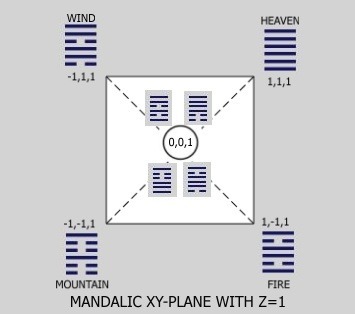
The circle in the center of this figure is intended to indicate that the two pairs of antipodal hexagrams at this central point of the cube face rotate through 90° four times consecutively to complete a 360° revolution. But I am describing the situation here in terms of revolution only to show an analogy to imaginary numbers.  The actual mechanisms involved can be better characterized as inversions (reflections through a point),  and the bottom line here is that for each diagonal of a square, the corresponding mandalic square has  a possibility of 4 diagonals;  for each diagonal of a cube,  the corresponding mandalic cube has a possibility of 8 diagonals. For computer science, such a multiplicity of possibilities offers a greater number of logic gates in the same computing space and the prospect of achieving quantum computing sooner than would be otherwise likely.^[7]

Similarly, the twelve edge centers of the ordinary cube host a single Cartesian point,  but the superposed mandalic cube hosts two hexagrams at the same point. These two hexagrams are always inverse hybrids of the two vertex hexagrams of the particular edge.  For example,  the edge with vertices  WIND over WIND  and  HEAVEN over HEAVEN  has as the two hybrid hexagrams  at the  center point  of the edge  WIND over HEAVEN  and HEAVEN over WIND. Since the two vertices of concern here connect with one another  via  the horizontal x-dimension,  the two hybrids  differ from the parents and one another only in Lines 1 and 4 which correspond to this dimension.  The other four Lines encode the y- amd z-dimensions, therefore remain unchanged during all transformations undergone in the case illustrated here.^[8]

This post began as a description of the structure of the mandalic coordinate system and how it differs from those of the complex plane and quaternions.  In the composition,  it became also  a passable introduction to the method of  composite dimension.  Additional references to the way composite dimension works  can be found scattered throughout this blog and Hexagramium Organum.  Basically the resulting construction can be thought of as a  tensegrity structure,  the integrity of which is maintained by opposing forces in equilibrium throughout, which operate continually and never fail,  a feat only nature is capable of.  We are though permitted to map the process  if we can manage to get past our obsession with  and addiction to the imaginary and complex numbers and quaternions.^[9]

In our next session we’ll flesh out probable dimension a bit more with some illustrative examples. And possibly try putting some lipstick on that PIG (Presumably Imaginary Garbage) to see if it helps any.

(continuedhere)

Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions  (A tesseract).  There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

Notes

[1] For more on this theme,  regarding quaternions,  see Footnote [1]  here. My own view is that imaginary numbers, complex plane and quaternions are artificial devices, invented by rational man, and not found in nature.  Though having limited practical use in  representation of rotations  in  ordinary space they have no legitimate application to quantum spaces,  nor do they have any substantive or requisite relation to square root, beyond their fortuitous origin in the Rationalists’ dissection and codification of square root historically, but that part of the saga was thoroughly misguided.   We wuz bamboozled.  Why persist in this folly? Look carefully without preconception and you’ll see this emperor’s finery is wanting. It is not imperative to use imaginary numbers to represent rotation in a plane. There are other, better ways to achieve the same. One would be to use sin and cos functions of trigonometry which periodically repeat every 360°.  (Read more about trigonometric functions here.)  Another approach would be to use polar coordinates.

[SOURCE]

A quaternion, on the other hand,  is a four-element vector composed of a single real element and three complex elements. It can be used to encode any rotation in a  3D coordinate system.  There are other ways to accomplish the same, but the quaternion approach offers some advantages over these.  For our purposes here what needs to be understood is that mandalic coordinates encode a hybrid 6D/3D discretized space. Quaternions are applicable only to continuous three-dimensional space.  Ultimately,  the two reside in different worlds and can’t be validly compared. The important point here is that each has its own appropriate domain of judicious application. Quaternions can be usefully and appropriately applied to rotations in ordinary three-dimensional space, but not to locations or changes of location in quantum space.  For description of such discrete spaces, mandalic coordinates are more appropriate, and their mechanism of action isn’t rotation but inversion (reflection through a point.) Only we’re not speaking here about inversion in Euclidean space, which is continuous, but in discrete space, a kind of quasi-Boolean space,  a higher-dimensional digital space  (grid or lattice space). In the case of an electron this would involve an instantaneous jump from one electron orbital to another.

[2] I think another laudatory feature of mandalic coordinates is the fact that they are based on a thought system that originated in human prehistory, the logic of the primal I Ching. The earliest strata of this monumental work are actually a compendium of combinatorics and a treatise on transformations,  unrivaled until modern times, one of the greatest intellectual achievements of humankind of any Age.  Yet its true significance is overlooked by most scholars, sinologists among them.  One of the very few intellectuals in the West who knew its true worth and spoke openly to the fact, likely at no small risk to his professional standing, was Carl Jung, the great 20th century psychologist and philosopher.

It is of relevance to note here that all the coordinate systems mentioned are, significantly,  belief systems of a sort.  The mandalic coordinate system  goes beyond the others though,  in that it is based on a still more extensive thought system, as the primal I Ching encompasses an entire cultural worldview.  The question of which,  if any,  of these coordinate systems actually applies to the natural order is one for science, particularly physics and chemistry, to resolve.

Meanwhile, it should be noted that neither the complex plane nor quaternions refer to any dimensions beyond the ordinary three, at least not in the manner of their current common usage.  They are simply alternative ways of viewing and manipulating the two- and three-dimensions described by Euclid and Descartes. In this sense they are little different from  polar coordinatesortrigonometry  in what they are attempting to depict.  Yes, quaternions apply to three dimensions, while polar coordinates and trigonometry deal with only two.  But then there is the method of  Euler angles  which describes orientation of a rigid body in three dimensions and can substitute for quaternions in practical applications.

A mandalic coordinate system, on the other hand, uniquely introduces entirely new features in its composite potential dimensions and probable numbers which I think have not been encountered heretofore. These innovations do in fact bring with them  true extra dimensions beyond the customary three  and also the novel concept of dimensional amplitudes.  Of additional importance is the fact that the mandalic method relates not to rotation of rigid bodies,  but to interchangeability and holomalleability of parts  by means of inversions through all the dimensions encompassed, a feature likely to make it useful for explorations and descriptions of particle interactions of quantum mechanics.  Because the six extra dimensions of mandalic geometry may, in some manner, relate to the six extra dimensions of the 6-dimensional Calabi–Yau manifold, mandalic geometry might equally be of value in string theoryandsuperstring theory.

Itis possible to use mandalic coordinates to describe rotations of rigid bodies in three dimensions,  certainly,  as inversions can mimic rotations, but this is not their most appropriate usage. It is overkill of a sort. They are capable of so much more and this particular use is a degenerate one in the larger scheme of things.

[3] This can be likened to a quark/gluon soup.  It is a unique and very special state of affairs that occurs here. Physicists take note. Don’t let any small-minded pure mathematicians  dissuade you from the truth.  They will likely write all this off as “sacred geometry.” Which it is, of course, but also much more.  Hexagram superpositions  and  stepwise dimensional transitions  of the mandalic coordinate system could hold critical clues  to  quantum entanglement and quantum gravity. My apologies to those mathematicians able to see beyond the tip of their noses. I was not at all referring to you here.

[4] Hopefully also with dimensions and points of the quaternion coordinate system once I understand the concepts involved better than I do currently. It should meanwhile be underscored that full comprehension of quaternions is not required to be able to identify some of their more glaring inadequacies.

[5] In speaking of  "existing at the same locale at different times"  I need to remind the reader and myself as well that we are talking here about  particles or other subatomic entities that are moving at or near the speed of light,- - -so very fast indeed. If we possessed an instrument that allowed us direct observation of these events,  our biologic visual equipment  would not permit us to distinguish the various changes taking place. Remember that thirty frames a second of film produces  the illusion of motion.  Now consider what  thirty thousand frames  a second  of  repetitive action  would do.  I think it would produce  the illusion of continuity or standing still with no changes apparent to our antediluvian senses.

[6] Each antipodal pair has four different possible ways of traversing the face center.  Similarly,  the mandalic cube has  thirty-two diagonals  because there are eight alternative paths by which an antipodal pair might traverse the cube center. This just begins to hint at the tremendous number of  transformational paths  the mandalic cube is able to represent, and it also explains why I refer to dimensions involved as  potentialorprobable dimensions  and planes so formed as probable planes.  All of this is related to quantum field theory (QFT), but that is a topic of considerable complexity which we will reserve for another day.

[7] One advantageous way of looking at this is to see that the probabilistic nature of the mandalic coordinate system in a sense exchanges bits for qubits and super-qubits through creation of different levels of logic gates that I have referred to elsewhere as different amplitudes of dimension.

[8] Recall that the Lines of a hexagram are numbered 1 to 6, bottom to top. Lines 1 and 4 correspond to, and together encode, the Cartesian x-dimension. When both are yang (+),  application of the method of  composite dimension results in the Cartesian value  +1;  when both yin (-),  the Cartesian value  -1. When either Line 1 or Line 4 is yang (+) but not both (Boole’s exclusive OR) the result is one of two possible  zero formations  by destructive interference. Both of these correspond to (and either encodes) the single Cartesian zero (0). Similarly hexagram Lines 2 and 5 correspond to and encode the Cartesian y-dimension; Lines 3 ane 6, the Cartesian z-dimension. This outline includes all 9 dimensions of the hybrid  6D/3D coordinate system:  3 real dimensions and the 6 corresponding probable dimensions. No imaginary dimensions are used; no complex plane; no quaternions. And no rotations. This coordinate system is based entirely on inversion (reflection through a point)  and on constructive or destructive interference. Those are the two principal mechanisms of composite dimension.

[9] The process as mapped here is an ideal one.  In the real world errors do occur from time to time. Such errors are an essential and necessary aspect of evolutionary process. Without error, no change. And by implication, likely no continuity for long either, due to external damaging and incapacitating factors that a natural world devoid of error never learned to overcome.  Errors are the stepping stones of evolution, of both biological and physical varieties.

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - II

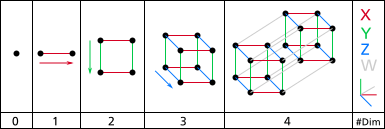
(continued from here)

When a geometric interpretation of imaginary numbers was at last proposed,  long after they were invented,  it was as though accomplished by central committee. The upshot was easily enough understood but also simplistic. In broad brushstroke here is what seems to have gone down.

The 3 dimensions of Descartes’ coordinate system-a number already deficient from the perspective of mandalic geometry-were reduced to just one.  Of the real number axes then  only the x-axis remained.  This meant from the get-go  that  any  geometric figure that ensued  could encompass only linearity in terms of real numbers and dimensions.  It was applicable only to a line segment,  so the complex plane that resulted  could describe just one real dimension and one imaginary dimension.  It consecrated the number line in a single dimension, to exclusion of its proper habitation in two others besides. Strike one for imaginary numbers.^[1]

With that as background let’s look now at the rotations described by this geometric interpretation of imaginary numbers in the context of the complex plane.

i in the complex or cartesian plane. Real numbers lie on the horizontal axis, and imaginary numbers lie on the vertical axis By Loadmaster (David R. Tribble) (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

The number 1 is the multiplicative identity element for real numbers and the number -1  is the  reflection inversion element  for real numbers.  Put another way, the number one times any number equals that number;  the number -1 times any number is  a negative of that number  or  the inverse number through a reference point, usually taken as zero. Multiplying by 1 then leaves 1, -1, i and -i all unchanged. Multiplying by -1  changes  -1 to 1, 1 to -1, i to -i, and -i to i.  In terms of rotations in the complex plane, these changes  all involve a rotation through 180 degrees.  Multiplication of the number 1 by i changes it to i; i by i changes it to -1; -1 by i to -i; and -i by i to 1.  These changes all involve rotations through 90 degrees.  And finally, multiplication of 1 by -i changes it to -i; -i by -i changes it to -1; -1 by -i to i; and i by -i to 1: all changes involving rotations through -90 degrees.

The figure below shows another way to interpret these rotations that amounts to the same tbing: i¹ = i; i² =-1; i³ = -i; i⁴ = 1.  Click to enlarge.

Four numbers on the real line multiplied by integer powers of the imaginary unit, which corresponds to rotations by multiples of the right angle. By Keφr [CC0],via Wikimedia Commons

I think a committee of some sort must have come up with this resplendent plan. For certain it was an Academy of Mathematics and Sciences that endorsed and enthroned it. All bow to central authority.

I had planned to include a comparison of imaginary numbers and probable numbers in this post as well but because that is a long discussion itself, it will have to wait till the next post.  I might add it should prove well worth the wait.

(continuedhere)

Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions  (A tesseract).  There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

Notes

[1] Mathematician William Rowan Hamilton  subsequently addressed this deficiency in 1843 with his  quaternions,  a  number system  that  extends the complex numbers to three-dimensional space.  Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space  or,  in other words, as the quotient of two vectors.  This complicated matters even more by introducing a non-commutative multiplication operation to the system, though to be fair the quaternion coordinate system has found some useful applications mainly for calculations involving 3-dimensional rotations,  as in 3-dimensional computer graphics,computer vision, and crystallographic texture analysis. Still it becomes problematic when theoretical physics attempts use of quaternions in calculations pertaining to  atomic and subatomic spaces  where rotations do not actually take place.  The conclusion to be drawn here is that quaternions can be usefully,  if somewhat clumsily,  applied to 3-dimensional macro-spaces but are inapproriate for accurate description of higher dimensional spaces. What is here unfortunate and misleading  is that quaternions apparently do describe outcomes of events in the quantum realm to some partial degree,  if not the mechanisms of the events themselves.  Physicists would not long tolerate them were that not so.

[ADDENDUM (24 APRIL, 2016)
Since writing this I’ve learned that quaternions are not currently used in quantum physics nor were they ever, to any great degree, in the past.]

In other words, sometimes  the right answer  can be reached by a wrong method. In the case under discussion here, we should note that it is possible for a rotation to mimic inversion (reflection through a point). A 90° rotation in two dimensions can mimic a single inversion in a single plane through an edge of a square, and a 180° rotation in two dimensions can mimic a single inversion through a diagonal of a square  or  two successive inversions  through  two perpendicular edges of a square.  A 180° rotation in three dimensions  can mimic three inversions through three mutually perpendicular edges of a square;  a combination of  one inversion through a diagonal of a square  and another through an edge perpendicular to the plane of the first inversion;  or a single inversion through a diagonal of the cube. Subatomic paricles exist as discrete or quantized entities and would follow such methods of transformation rather than rotations through a continuous space.  Of course, transformations involving a diagonal would require more transformative energy than one involving a single edge.

Such patterns of relationship and transformation could no doubt be described in terms of quantum states and quantum numbers without too much difficulty by a knowledgeable theoretical physicist.  Surely doing so could be no more difficult than using quaternions,  which may give a correct answer while also misleading and limiting knowledge of the the true workings of the quantum realm by using an incorrect mechanism, one non-commutative to boot. Nature doesn’t approve of hat tricks like that.