#force fields

“Finally! It’s been hours, but we’ve finally been dug out!”

“About time.” The villain muttered and pressed a sharp piece of debris against Hero’s neck.

“Are you kidding me? I thought we built a real connection back there.”

“Nothing personal, but I need a shield to keep the police from arresting me.”

“You’re the worst.”

“Yes I know.”

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - II

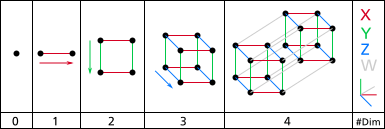
(continued from here)

When a geometric interpretation of imaginary numbers was at last proposed,  long after they were invented,  it was as though accomplished by central committee. The upshot was easily enough understood but also simplistic. In broad brushstroke here is what seems to have gone down.

The 3 dimensions of Descartes’ coordinate system-a number already deficient from the perspective of mandalic geometry-were reduced to just one.  Of the real number axes then  only the x-axis remained.  This meant from the get-go  that  any  geometric figure that ensued  could encompass only linearity in terms of real numbers and dimensions.  It was applicable only to a line segment,  so the complex plane that resulted  could describe just one real dimension and one imaginary dimension.  It consecrated the number line in a single dimension, to exclusion of its proper habitation in two others besides. Strike one for imaginary numbers.^[1]

With that as background let’s look now at the rotations described by this geometric interpretation of imaginary numbers in the context of the complex plane.

i in the complex or cartesian plane. Real numbers lie on the horizontal axis, and imaginary numbers lie on the vertical axis By Loadmaster (David R. Tribble) (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

The number 1 is the multiplicative identity element for real numbers and the number -1  is the  reflection inversion element  for real numbers.  Put another way, the number one times any number equals that number;  the number -1 times any number is  a negative of that number  or  the inverse number through a reference point, usually taken as zero. Multiplying by 1 then leaves 1, -1, i and -i all unchanged. Multiplying by -1  changes  -1 to 1, 1 to -1, i to -i, and -i to i.  In terms of rotations in the complex plane, these changes  all involve a rotation through 180 degrees.  Multiplication of the number 1 by i changes it to i; i by i changes it to -1; -1 by i to -i; and -i by i to 1.  These changes all involve rotations through 90 degrees.  And finally, multiplication of 1 by -i changes it to -i; -i by -i changes it to -1; -1 by -i to i; and i by -i to 1: all changes involving rotations through -90 degrees.

The figure below shows another way to interpret these rotations that amounts to the same tbing: i¹ = i; i² =-1; i³ = -i; i⁴ = 1.  Click to enlarge.

Four numbers on the real line multiplied by integer powers of the imaginary unit, which corresponds to rotations by multiples of the right angle. By Keφr [CC0],via Wikimedia Commons

I think a committee of some sort must have come up with this resplendent plan. For certain it was an Academy of Mathematics and Sciences that endorsed and enthroned it. All bow to central authority.

I had planned to include a comparison of imaginary numbers and probable numbers in this post as well but because that is a long discussion itself, it will have to wait till the next post.  I might add it should prove well worth the wait.

(continuedhere)

Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions  (A tesseract).  There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

Notes

[1] Mathematician William Rowan Hamilton  subsequently addressed this deficiency in 1843 with his  quaternions,  a  number system  that  extends the complex numbers to three-dimensional space.  Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space  or,  in other words, as the quotient of two vectors.  This complicated matters even more by introducing a non-commutative multiplication operation to the system, though to be fair the quaternion coordinate system has found some useful applications mainly for calculations involving 3-dimensional rotations,  as in 3-dimensional computer graphics,computer vision, and crystallographic texture analysis. Still it becomes problematic when theoretical physics attempts use of quaternions in calculations pertaining to  atomic and subatomic spaces  where rotations do not actually take place.  The conclusion to be drawn here is that quaternions can be usefully,  if somewhat clumsily,  applied to 3-dimensional macro-spaces but are inapproriate for accurate description of higher dimensional spaces. What is here unfortunate and misleading  is that quaternions apparently do describe outcomes of events in the quantum realm to some partial degree,  if not the mechanisms of the events themselves.  Physicists would not long tolerate them were that not so.

[ADDENDUM (24 APRIL, 2016)
Since writing this I’ve learned that quaternions are not currently used in quantum physics nor were they ever, to any great degree, in the past.]

In other words, sometimes  the right answer  can be reached by a wrong method. In the case under discussion here, we should note that it is possible for a rotation to mimic inversion (reflection through a point). A 90° rotation in two dimensions can mimic a single inversion in a single plane through an edge of a square, and a 180° rotation in two dimensions can mimic a single inversion through a diagonal of a square  or  two successive inversions  through  two perpendicular edges of a square.  A 180° rotation in three dimensions  can mimic three inversions through three mutually perpendicular edges of a square;  a combination of  one inversion through a diagonal of a square  and another through an edge perpendicular to the plane of the first inversion;  or a single inversion through a diagonal of the cube. Subatomic paricles exist as discrete or quantized entities and would follow such methods of transformation rather than rotations through a continuous space.  Of course, transformations involving a diagonal would require more transformative energy than one involving a single edge.

Such patterns of relationship and transformation could no doubt be described in terms of quantum states and quantum numbers without too much difficulty by a knowledgeable theoretical physicist.  Surely doing so could be no more difficult than using quaternions,  which may give a correct answer while also misleading and limiting knowledge of the the true workings of the quantum realm by using an incorrect mechanism, one non-commutative to boot. Nature doesn’t approve of hat tricks like that.