#probable numbers

Can a number system be both the new kid on the block and older than written history?

The real number system as it exists today has been with us for a few centuries.  In foundation it is monovalent,  monophasic,  and sequential.

The probable number system dates to prehistory but was lost in the mists of time until recently rediscovered and resurrected.  In contrast to the real number system it is foundationally bivalent, biphasic, and cyclic.

The probable number system has considerably more structure than the real number system and is therefore more robust.  In this sense, it is similar to the complex number system.

In contrast to the complex number system,  the probable number system in its foundation presupposes that numbers can assume wavelike forms capable of  constructive and destructive interference  operationally through the compositing of higher to lower dimension.

By means of compositing of dimension probable numbers are able to  distribute  throughout the entire  mandalic unit vector cube  (which is structurally a  superposition  of  the 6-dimensional unit vector hypercube on the 3-dimensional unit vector cube) a function analogous in important ways  to that performed in the complex number system by the centralized imaginary unit i.

Another important way in which the probable number system differs from both the real number system and the complex number system is the absence of  nothingness  and the zero representing it.  In its place we find the concepts of  balance and equilibrium.  Nullification still exists in form of annihilation and its opposite in the form of creation.  But the Cartesian coordinate system  of ordered pairs and ordered triads  is transformed by this approach to handling number and dimension  from a ring into a field of hyperdimensional numbers over real numbers in three dimensions.

(to be continued)

© 2016 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 315-

A Recap of Some Important Ideas Regarding Mandalic Geometry

1. Mandalic geometry (MG) is a new kind of mathematical methodology based on a worldview having roots that predate written history.
2. It is a discrete geometry which currently consists of just a coordinate system but can be extended as Descartes did his to encompass an entire analytic geometry.
3. Mandalic geometry introduces and is based on a new number system, the probable number system (or probabilistic number system.)
4. Just as the complex number system combines real numbers and imaginary numbers and is more robust than either, the probable number system combines real numbers and probable numbers and is more robust than either.
5. The probable number system is also more robust than the complex number system. Complex numbers combine real numbers with imaginary numbers to form the single complex plane. Composite numbers combine real numbers with probable numbers to form six interdependent composite planes.
6. Axiomatic to the system is the contention that numbers can exist in different dimensions and therefore can be described as being of some particular dimension. Numbers are always viewed and treated within context of a stated dimension.
7. Probable numbers are an extension of the real numbers to higher dimensions and are independent of imaginary and complex numbers.
8. Mandalic geometry does not admit the existence of square root of -1 in the real world other than in mathematics invented by the human mind. In place of square root of negative numbers, MG introduces the new concept of contra-square root. In brief this involves substitution of a combination form of interactive two-dimensional analogues of +1 and -1 for -1 as currently used in imaginary number contexts. This is more fully explained elsewhere in the blog.
9. Put another way, in place of imaginary numbers MG posits the existence of probable numbers. These can be considered the result of what is essentially wavelike interactions of higher dimensional numbers to form the real numbers we know in the 3-dimensional world.
10. Higher dimensional numbers can interact with one another through wavelike constructive and destructive interference to generate ordinary
    3-dimensional numbers. Numbers are not viewed as constants to be acted upon as Descartes so views them but rather as being themselves active and changeable. They participate in process. This feature alone enables composite numbers to mediate between mathematics and physics better than either real or complex numbers can.
11. The interactions of higher dimensional numbers in the process of dimensional compositing to yield 3-dimensional numbers is a function of time and therefore probabilistic from our limited ordinary point of view. From this perspective, certain probablity distributions are the result of dimensional compositing and the consequent mandalic form. MG considers the probabilistic nature of quantum mechanics likely to be based on such.
12. The probabilistic nature in three dimensions of what are here called probable numbers is what gives rise to the mandalic form which can in a sense be considered the 3-dimensional evolution of 6-dimensional numbers from protean representations through progressive differentiation of form to the stage of maximal differentiation and back again to the undifferentiated state of greatest probability.
13. The mandalic form has a geometric progression of its line structures in the three Euclidean/Cartesian dimensions such that series of numbers of the form 1:2:1, 2:4:2, and 4:8:4 occur throughout all of those dimensions when a hybrid 6D/3D coordinate system results from performing 2:1 compositing from six to three dimensions.
14. Mandalic geometry views points and lines in three dimensions as convenient fictions that exist only as evanescent probabilistic concurrences of analogous entities in higher dimensions.
15. The probabilistic nature of MG makes it ideal for investigations and descriptions of quantum mechanics.
16. The exclusion of imaginary and complex numbers and substitution of probable and composite numbers which are easily reducible to ordinary algebraic/arithmetic forms and can be worked with using the same methods as those mathematical disciplines makes MG more utilitarian and appropriate to application to quantum mechanics than are complex numbers. All operations performed are based on simple inversion (reflection through a point) and on real numbers, maintaining all the usual rules and properties of ordinary arithmetic, including commutativity (which quaternions fail to preserve.)
17. MG is currently based on discrete numbers and is concerned mainly with the positive and negative integers. Fractions and irrational numbers are not excluded from the system but do not currently play a significant role. Future incarnations of MG will extend it outward beyond the unit vector cube to tile the geometric universe and inward to encompass fractional entities and fractals.
18. It is a hybrid geometry resulting from superposition of 6-dimensional numbers and 3-dimensional numbers and is fully commensurate with
    3-dimensional Cartesian geometry.
19. It describes a linear mapping of two dimensions to one dimension which forms a field of probable numbers over the field of real numbers, analogous to the field of complex numbers but constructed on a different principle and extending to the real numbers in all three Cartesian dimensions rather than just one. The two independent higher dimensions so mapped become dependent variables in the mandalic “line” that results from the compositing of the two. This is expressed, in a sense, as two sine waves 180 degrees out of phase that mutually intersect a common Cartesian axis (x,y or z) at Cartesian +1 and -1 and are maximally separated at Cartesian 0.
20. This phase difference produces wave interference of both constructive and destructive varieties. So-called “points” or “particles” they represent come into existence only discretely and intermittently at Cartesian -1, +1, and 0, the locations of intersection or confluence (-1 and +1) and maximum separation, the maxima/minima of the two entangled sine waves that occur at Cartesian 0.
21. As the unit vector cube corresponds to and describes only half of each of the two sine waves, two unit vector cubes are required for a full cycle. Mandalic geometry as currently formulated with a single unit cube then needs to be extended to at least two of these. Extension in both directions of all three Cartesian axes is easily accomplished by repeatedly inverting the current single unit vector cube.
22. This means that mandalic coordinates alternate positive and negative on both sides of Cartesian 0. The extensions can be continued to infinity in both directions, but not, properly speaking, positive and negative infinity since the manner of extension has created what is essentially a convention-free coordinate system which consists of repeated units of consecutively inverted unit vector cubes in which positive and negative alternate ad infinitum and every Cartesian even-numbered coordinate becomes a “zero equivalent” , or better, a neo-zero in this extended mandalic coordinate system.
23. The resulting geometry is a dynamic one with “points”, “lines”, and “planes” coming into and passing out of existence intermittently in a time-sharing of corresponding Cartesian entities. It “persists” in time and space by means of continuous creation, destruction and re-creation and is “held together” by “force fields” produced and maintained by means of tensegrity which is based ultimately on dimension and number, and by a process that.might best be described as a “weaving of reality” with warp and woof.
24. The 2:1 compositing of dimension involved creates a new number system the members of which are like the real integers in all ways except that they map differently to a Cartesian geometric space. Whereas Decartes assumes that one number maps to one point, MG does not make this assumption which is just an unproved axiom that Descartes makes implicit use of.
25. The method of dimensional compositing automatically results in a mandalic formation having a geometric progression through three Euclidean/Cartesian dimensions from periphery to center (origin).
26. Currently MG is limited to a description of unit vectors in a composite hybrid 6D/3D geometry but can be extended to include all scalar values and any even number of dimensions.
27. The notation system used is borrowed from Taoism and foreign to most Western mathematicians. It is, however, basically equivalent to Cartesian coordinate signs (yin=minus; yang=plus); ordered pairs (=bigrams); and ordered triads (=trigrams); and extends these concepts to include ordered quads (=tetragrams) and ordered sextuplets (=hexagrams).
28. This notation system is used rather than the usual Cartesian notation because it is much easier for the mind to manipulate dimensional numbers using it. It takes only a little practice to become accustomed to using it. Without its use, understanding of mandalic geometry becomes extremely difficult, if not impossible.
29. As MG views a point as a concurrence of various different dimensions, it interprets Cartesian ordered pairs and triads, and their extensions to higher dimensions, as tensors and treats them as such. This makes it possible to apply operations of addition and multiplication to these mathematical entities in a manner analogous to the way William Rowan Hamilton applied these operations to complex numbers by way of what he called “algebraic couples”.
30. The probabilistic mandalic form that is the hallmark of MG conveys and necessitates a new interpretation of zero(0). In MG “zero” is not the empty null that it is in Cartesian geometry and Western mathematics generally, but rather a fount of being, so to speak, and a logic gate spanning dimensions. Wherever a zero occurs in Cartesian coordinates two Cartesian-equivalent forms are found in mandalic coordinates. So in the mandalic cube based on unit vectors the twelve edge centers, having a single Cartesian zero, have two Cartesian-equivalent forms (hexagrams); the six face centers, having two Cartesian zeros, have four Cartesian-equivalent forms; and the single cube center, the Cartesian origin point with three zeros, has eight Cartesian-equivalent forms.
31. Thisalternative zero and the mandalic structure it inhabits force the creation of four different amplitudes of dimension in the 6-dimensional unit vector cube. These are not independent but all mutually dependent and holo-interactive within the composite 6D/3D coordinate system. All of this occurs in a context reminiscent of the one inhabited by nuclear particles. The mapping proposed by MG may in fact model the elementary force fields, electromagnetism and quantum chromodynamics. It suggests a possible mechanism for formation of the state of matter known as a quark-gluon plasma. Hidden within it may even be the secret of quantum gravity.

© 2016 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 312-

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - VI

(continued from here)

“O Oysters, come and walk with us!” The Walrus did beseech. “A pleasant walk, a pleasant talk, Along the briny beach: We cannot do with more than four, To give a hand to each.”

* * *

“The time has come,” the Walrus said, “To talk of many things: Of shoes–and ships–and sealing-wax– Of cabbages–and kings– And why the sea is boiling hot– And whether pigs have wings.”

-Lewis Carroll, The Walrus and the Carpenter

In this segment, probable numbers will be shown to grow out of a natural context inherently rather than through geometric second thought as transpired  in the history of Western thought  with imaginary numbers and complex plane.  To continue  with development of probable numbers it will be necessary to leave behind,  for the time being,  all preoccupation with imaginary numbers and complex plane.  It will also be necessary  to depart from our comfort zone of Cartesian spatial coordinate axioms and orientation.

Probable coordinates do not negate validity of Cartesian coordinates but they do relegate them to the status of a special case.  In the probable coordinate system the three-dimensional coordinate system of Descartes maps only one eighth of the totality. This means then, that the Cartesian two-dimensional coordinate plane furnishes just one quarter of the total number of  corresponding probable coordinate mappings  projected to a two-dimensional space.^[1]  It suggests also that  Cartesian localization  in 2-space or 3-space is just a small part of the whole story regarding actual spatial and temporal locality and their accompanying physical capacities, say for instance of momentum or mass, but actually encompassing a host of other competencies as well.

Although this might seem strange it is a good thing. Why is it a good thing?  First, because nature, as a self-sustaining reality, cannot favor any one coordinate scheme but must encompass all possible - if it is to realize any.  Second,  because both the Schrödinger equationandFeynman path integral approaches to quantum mechanics say it is so.^[2]  Third,  because Hilbert space demands it.  This may leave us disoriented and bewildered, but nature revels in this plan of probable planes. Who are we to argue?

So how do we accomplish this feat? Well, basically by reflections in all dimensions and directions. We extend the Cartesian vectors every way possible.  That would give us  a 3 x 3 grid or lattice  of coordinate systems (the original Cartesian system  and  eight new grid elements surrounding it),  but there are only four different types,  so we require only four of the nine to demonstrate. It is best not to show all nine in any case because to do so  would place our Cartesian system at direct center of this geometric probable universe and that would be misleading. Why? Because when we tile the two-dimensional universe to infinity in all directions,  there is no central coordinate system. Any one of the four could be considered at the center, so none actually is. Overall orientation is nondiscriminative.^[3]

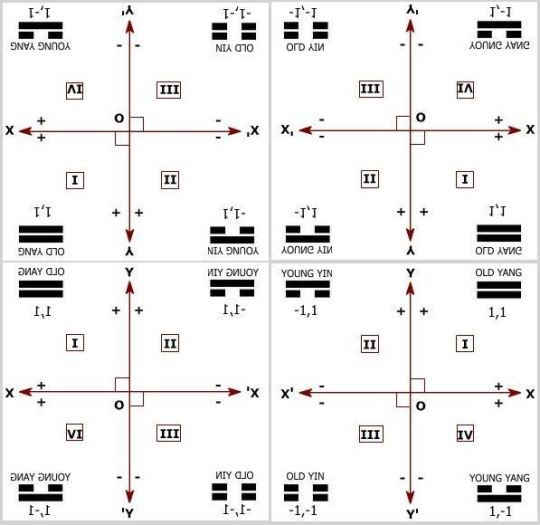
LOOKING GLASS CARTESIAN COORDINATE QUARTET

The image seen immediately above shows four  Looking House Cartesian coordinate systems, correlated within a mandalic plane. This mandalic plane is  one of six faces of a mandalic cube,  each of which  is constructed to a different plan but composed of similar building blocks, the four bigrams in various positions and orientations. A 2-dimensional geometric universe can be tiled with this image,  recursively repeating it in all directions throughout the two dimensions.^[4] It should not be very difficult for the reader to determine which of the four mandalic moieties references our particular conventional Cartesian geometric universe.^[5]

It remains only to be added here and now that potential dimensions, probable planes,  and  probable numbers  arise  immediately and directly from the remarks above. In some ways it’s a little like valence in chemical reactions.  We’ll likely take a look at that combinatory dynamic in context of mandalic geometry at some time down the road.  Next though we want to see how the addition of composite dimension impacts and modifies the basic geometry of the probable plane discussed here.^[6]

(to be continued)

Top image: The four quadrants of the Cartesian plane.  These are numbered in the counterclockwise direction by convention. Architectonically, two number lines are placed together, one going left-right and the other going up-down to provide context for the two-dimensional plane.  This image has been modified from one found here.

Notes

[1] To clarify further:  There are eight possible Cartesian-like orientation variants in mandalic space arranged around a single point at which they are all tangent to one another. If we consider just the planar aspects of mandalic space,  there are  four possible Cartesian-like orientation variants  which are organized about a central shared point in a manner similar to how quadrants are symmetrically arranged  about the Cartesian origin point (0,0) in ordinary 2D space. But here the center point determining symmetries is always one of the points showing greatest rather than least differentiation. That is to say it is formed by Cartesian vertices, ordered pairs having all 1s, no zeros.  That may have confused more than clarified, but it seemed important to say.  We will be expanding on these thoughts in posts to come. Don’t despair. For just now the important takeaway is that the mandalic coordinate system combines two very important elements that optimize it for quantum application:  it manages to be both probabilistic and convention-free  (in terms of spatial orientation,  which surely must relate to quantum states and numbers in some as yet undetermined manner.) At the same time, imaginary numbers and complex plane are neither.

[2] Even if physics doesn’t yet (circa 2016) realize this to be true.

[3] It is an easy enough matter to extrapolate this mentally to encompass the Cartesian three-dimensional coordinate system but somewhat difficult to demonstrate in two dimensions.  So we’ll persevere with a two-dimensional exposition for the time being. It only needs to be clarified here that the three-dimensional realization involves a 3 x 3 x 3 grid but requires just eight cubes to demonstrate because there are only eight different coordinate system types.

[4] I am speaking here in terms of ordinary dimensions but it should be understood that the reality is that the mandalic plane is a composite 4D/2D geometric structure, and the mandalic cube is a composite 6D/3D structure. The image seen here does not fully clarify that because it does not yet take into account composite dimension nor place the bigrams in holistic context within tetragrams and hexagrams.  All that is still to come.  Greater context will make clear how composite dimension works and why it makes eminent good sense for a self-organizing universe to invoke it. Hint: it has to do with quantum interference phenomena and is what makes all process possible.

ADDENDUM (12 APRIL, 2016)
The mandalic plane I am referring to here corresponds to the Cartesian 2-dimensional plane and is based on four extraordinary dimensions that are composited to the ordinary two dimensions, hence hybrid 4D/2D. It should be understood though that any number of extra dimensions could potentially be composited to two or three ordinary dimensions. The probable plane described in this post is not such a mandalic plane as no compositing of dimensions has yet been performed. What is illustrated here is an ordinary 2-dimensional plane that has undergone reflections in x- and y-dimensions of first and second order to form a noncomposited probable plane. The distinction is an important one.

[5] This is perhaps a good place to mention that the six  planar faces  of the mandalic cube fit together seamlessly in 3-space,  all mediated by the common shared central point, in Cartesian terms the origin at ordered triad (0.0.0) where eight hexagrams coexist in mandalic space. Moreover the six planes fit together mutually by means of a nuclear particle-and-force equivalent of the mortise and tenon joint but in six dimensions rather than two or three, and both positive and negative directions for each.

[6] It should also be avowed that tessellation of a geometric universe with a nondiscriminative, convention-free coordinate system need not exclude use of Cartesian coordinates entirely in all contextual usages.  Where useful they can still be applied in combination with mandalic coordinates since the two can be made commensurate,  irrespective of  specific Cartesian coordinate orientation locally operative. Whatever the Cartesian orientation might be it can always be overlaid with our conventional version of the same. More concretely, hexagram Lines can be annotated with an ordinal numerical subscript specifying Cartesian location in terms of our  local convention  should it prove necessary or desirable to do so for whatever reason.

On the other hand,  before prematurely throwing out the baby with the bath water, we might do well to ask ourselves whether these strange juxtapositions of coordinates might not in fact encode the long sought-after hidden variables that could transform quantum mechanics into a complete theory.  In mandalic coordinates of the reflexive nature described, these so-called hidden variables could be hiding in plain sight.  Were that to prove the case,  David Bohm andLouis de Broglie  would be  immediately and hugely vindicated  in advancing their  pilot-wave theory of quantum mechanics.  We could finally consign the Copenhagen Interpretation to the scrapheap where it belongs,  along with both imaginary numbers and the complex plane.

ADDENDUM (24 APRIL, 2016)
Since writing this I’ve learned that de Broglie disavowed Bohm’s pilot wave theory upon learning of it in 1952. Bohm had derived his interpretation of QM from de Broglie’s original interpretation but de Broglie himself subsequently converted to Niels Bohr’s prevailing Copenhagen interpretation.

© 2016 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 311-

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - V

(continued from here)

The four Cartesian quadrants provide the two-dimensional analogue of the number line and its graphic representation in Cartesian coordinate space.  This is the true native habitat of the square and, by implication, of square root.  Because  Enlightenment mathematicians  found fit to define square root in a different context inadvertently  -that of the number line- we will find it necessary to devise a different name for what ought rightly to have been called square root,  but wasn’t.  I propose that we retain the existent definition of tradition and refer to the new relationship between opposite numbers in the square,  that is to say,  opposite vertices through two dimensions or antipodal numbers, as contra-square root.^[1]

Modified from image found here.

Given this fresh context - one of greater dimension than the number line - it soon becomes clear with little effort that a unit number^[2]ofany dimension multiplied by itself gives as result the identity element of that express dimension. For the native two-dimensional context of the square the identity element is OLD YANG,  the bigram composed of two stacked yang (+) Lines,  which corresponds to yang (+1),  the identity element in the  one-dimensional context  of the number line. In a three-dimensional context,  the identity element is the trigram HEAVEN which is composed of three stacked yang (+) Lines.  The crucial idea here is that the identity element differs for each dimensional context,  and whatever that context might be,  it produces no change when in the operation of multiplication it acts as operator on any operand within the stated dimension.^[3]

As a corollary it can be stated that any number in any dimension n composed of  any combination  of  yang Lines (+1) and yin Lines (-1) if multiplied by itself (i.e., squared) produces the identity element for that dimension.  In concrete terms this means, for example, that any bigram multiplied by itself equals the bigram OLD YANG; any of eight trigrams multiplied by itself  equals the trigram HEAVEN;  and  any of the sixty-four hexagrams multiplied by itself  equals the hexagram HEAVEN; etc. (valid for any and all dimensions without exception). Consequently, the number of roots the identity element has in any dimension n is equal to the number 2ⁿ, these all being real roots in that particular dimension.

Similar contextual analysis would show that the inversion element of any dimension n  has  2ⁿ roots of the kind we have agreed to refer to as contra-square roots in deference to the Mathematics Establishment.^[4]

That leads us to the possibly startling conclusion that in every dimension n  there is an  inversion element  that has the same number of roots as the identity elementandall of them are real roots.  For two dimensions the two pairs that satisfy the requirement are bigram pairs

For one dimension there is only a single pair that satisfies. That is (surprise, surprise)  yin(-1)/yang (+1).  What it comes down to is
this:

If we are going to continue to insist on referring to square root
in terms of the one-dimensional number line, then

• +1 has two real roots of the traditional variety, +1 and -1
• -1 has two real roots of the newly defined contra variety,
  +1/-1 and -1/+1

So where do imaginary numbers and quaternions fit in all this? The short answer is they don’t.  Imaginary numbers entered the annals of human thought through error.  There was a pivotal moment^[5]  in the history of mathematics and science, an opportunity to see that there are in every dimension two different kinds of roots - - - what has been called square root and what we are calling contra-square roots.  Enlightenment mathematicians and philosophers  essentially allowed the opportunity to slip through their fingers unnoticed.^[6]

Descartes at least saw through the veil.  He called the whole matter of imaginary numbers ‘preposterous’.  It seems his venerable opinion was overruled though. Isaac Newton had his say in the matter too. He claimed that roots of imaginary numbers “had to occur in pairs.” And yet another great mathematician, philosopher opined.  Gottfried Wilhelm Leibniz,  in 1702 characterized √−1 as  “that amphibian between being and non-being which we call the imaginary root of negative unity.” Had he but preserved such augury conspicuously in mind he might have elaborated the concept of probable numbers in the 18th century.  If only he had truly understood the I Ching,  instead of dismissing it as a primitive articulation of his own binary number system.

(continuedhere)

Image: The four quadrants of the Cartesian plane. By convention the quadrants are numbered in a counterclockwise direction.  It is as though two number lines were placed together, one going left-right, and the other going up-down to provide context for the two-dimensional plane. Sourced from Math Is Fun.

Notes

[1] My preference might be for square root to be redefined from the bottom up, but I don’t see that happening in our lifetimes. Then too this way could be better.

[2] By the term unit number,  I intend any number of a given dimension that consists entirely of variant elements of the number one (1) in either its positive or negative manifestation.  Stated differently,  these are vectors having various different directions within the dimension,  but all of scalar value -1 (yin) or +1 (yang). All emblems of I Ching symbolic logic satisfy this requirement. These include the Line, bigram, trigram, tetragram, and hexagram.  In any dimension n there exist 2ⁿ such emblems.  In sum, for our purposes here, a unit number is any of the set of numbers, within any dimension n, which when self-multiplied (squared) produces the multiplicative identity of that dimension which is itself, of course, a member of the set.

ADDENDUM (01 MAY 2016): I’ve since learned that mathematics has a much simpler way of describing this. It calls all these unit vectors. Simple, yes?

[3] I think it fair to presume that this might well have physical correlates in terms of quantum mechanical states or numbers. Here’s a thought: why would it be necessary that all subatomic particles exist in the same dimension at all times given that they have a playing field of multiple dimensions, - some of them near certainly beyond the three with which we are familiar? And why would it not be possible for two different particles to be stable and unchanging in their different dimensions,  yet become reactive and interact with one another when both enter the same dimension or same amplitude of dimension?

[4] Since in any contra-pair (antipodal opposites) of any dimension, either member of the pair must be regarded  once as operator  and  once as operand. So for the two-dimensional square, for example, there are two antipodal pairs (diagonals) and either vertex of each can be either operator or operand.  So in this case, 2 x 2 = 4.  For trigrams there are four antipodal pairs, and 2 x 4 = 8. For hexagrams there are thirty-two antipodal pairs and 2 x 32 = 64. In general, for any dimension n there are 2 x 2ⁿ/2 = 2ⁿ antipodal pairs or contra-roots.

[5] Actually lasting several centuries, from about the 16th to the 19th century. Long enough,  assuredly,  for the error  to have been  discovered and corrected. Instead,  the 20th century dawned with error still in place,  and physicists eager to explain the newly discovered bewildering quantum phenomena compounded the error  by latching onto  √−1 and quaternions  to assuage their confusion and discomfiture.  This probably took place in the early days of quantum mechanics when the Bohr model of the atom still featured electrons as traveling in circular orbits around the nucleus or soon thereafter, visions of minuscule solar systems still fresh in the mind. At that time rotations detailed by imaginary numbers and quaternions may have still made some sense. Such are the vagaries of history.

[6] I think an important point to consider is that imaginary and complex numbers were, -to mathematicians and physicists alike,- new toys of a sort that  enabled them  to  accomplish certain things  they could not otherwise. They were basically tools of empowerment which allowed manipulation of numbers and points on a graph more easily or conveniently.  They provided
their controllers a longed for power over symbols, if not over the real world itself. In the modern world ever more of what we humans do and want to do involves manipulation of symbols. Herein,  I think,  lies the rationale for our continued fascination with and dependence on these tools of the trade. They don’t need to actually apply to the world of nature,  the noumenal world,  so long as they satisfy human desire for domination  over the world of symbols it has created for itself and in which it increasingly dwells, to a considerable degree apart from the natural world’s sometimes seemingly too harsh laws.

© 2016 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 310-

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - IV

(continued from here)

One of the notable things the Rationalists  failed to take into account in their analysis and codification of square roots  was  the significance of context. In so doing they assured that all related concepts they developed would eventually degenerate into a series of errors of conflation.  Do  not ever underestimate the importance of context.

Mathematicians, for example, can show that for any 3-dimensional cube  there exists  a  2-dimensional square,  the area of which equals the volume of the cube.^[1] And although that is true, something has been lost in translation. This is another of the sleights of hand mathematicians are so fond of.  Physicists cannot afford to participate in such parlor tricks as these, however mathematically true they might be.^[2]

We will begin now, then, to examine how the mandalic coordinate approach stacks up against that of imaginary numbers and quaternions. The former are holistic and respective of the natural order; the latter are irresponsibly rational, simplistic and, in final analysis, wrong about how nature works.^[3] Ambitious endeavor indeed, but let’s give it a go.

We’ve already looked at how the standard geometric interpretation of imaginary numbers in context of the complex plane is based on rotations through continuous Euclidean space.  You can brush up on that aspect of the story here if necessary. The mandalic approach to mapping of space is more complicated and far more interesting.  It involves multidimensional placement of elements in a discrete space, which is to say a discontinuous space,  but one fully commensurate with both Euclidean and Cartesian 3-dimensional space. The holo-interactive manner in which these elements relate to one another leads to a  probabilistic mathematical design  which preserves commutative multiplication,  unlike quaternions which forsake it.

Transformations between these elements are based on inversion (reflection through a point) rather than rotation which cannot in any case reasonably apply to discrete spaces.  The spaces that quantum mechanics inhabits are decidedly discrete.  They cannot be accurately detailed using imaginary and complex numbers or quaternions.  To discern the various, myriad transitions which can occur among mandalic coordinates requires some patience. I think it cannot be accomplished overnight but at least in the post next up we can make a start.^[4]

(continuedhere)

Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions  (A tesseract).  There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

Notes

[1] If only in terms of scalar magnitude. Lost in translation are all the details relating to vectors and dimensions in the original.  Conflation does not itself in every case involve what might be termed ‘error’ but because it always involves loss or distortion of information,  it is nearly always guaranteed to eventuate in error somewhere down the line of argument. The point of all this in our context here is that, in the history of mathematics, something of this sort occurred when the Rationalists of the Enlightenment invented imaginary and complex numbers and again when quaternions were invented in 1843. These involved a disruption of vectors and dimensions as treated by nature. The loss of information involved goes a long way in explaining why no one has been able to explain whyandhow quantum mechanics works in a century or more.  These  misconstrued theses  of mathematics behave like a demon or ghost in the machine that misdirects,  albeit unintentionally, all related thought processes.  What we end up with is a plethora of confusion. The fault is not in quantum mechanics but in ourselves, that we are such unrelentingly rational creatures, that so persistently pursue an unsound path that leads to reiterative error.

[2] Because physicists actually care about the real world; mathematicians, not so much.

[3] It must be admitted though that it was not the mathematicians who ever claimed imaginary numbers had anything to do with nature and the real world. Why would they? Reality is not their concern or interest. No, it was physicists themselves who made the mistake. The lesson to be learned by physicists here I expect is to be careful whose petticoat they latch onto. Not all are fabricated substantially enough to sustain their thoughts about reality, though deceptively appearing to do just that for protracted periods of time.

[4] My apologies for not continuing with this here as originally intended. To do so would make this post too long and complicated. Not that transformations among mandalic coordinates are difficult to understand,  just that they are very convoluted. This is not a one-point-encodes-one-resident-number plan like that of Descartes we’re talking about here. This is mandala country.

© 2016 Martin Hauser

Please note:  The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)

Scroll to bottom for links to Previous / Next pages (if existent).  This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added.  To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering.  To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)

-Page 309-

Beyond the Enlightenment Rationalists:
From imaginary to probable numbers - I

Imaginary numbers arose in the history of mathematics as a result of misunderstanding the dimensional character of numbers.  There was a failure to acknowledge that numbers exist in a context of dimension. This has earlier been addressed at length.^[1]  Simply put, numbers exist always in a particular dimensional context.  Square numbers pertain to a context of two dimensions and therefore to a plane,  not a line.  Square roots then ought justly reference a two-dimensional geometrical context rather than the linear one mathematics has maintained ever since mathematicians of the Age of Enlightenment decreed it so.  Square roots contrary to the way mathematics would have it can neither exist in nor be found in any single line segment,  because they do not originate in the number line but in the two-dimensional square.

Algebra, not geometry, provided the breeding ground for imaginary numbers.  They were given a geometric interpretation as an afterthought only, long after the fact of their invention. Rationalist algebraists, feeling compelled to give meaning to equations of the form b² = -4 came up with the fantastic notion of imaginary numbers. Only indirectly did these grow out of nature, by way of minds of men obsessed with reason.^[2]

Descartes knew of the recently introduced square roots of negative numbers. He thought them preposterous and was first to refer to the new numbers by the mocking name imaginary, a label which stuck and which continues to inform posterity of the exact manner in which he viewed the oddities.  It is one of the ironies of history that when at last a geometrical interpretation of square root of negative numbers was offered it involved swallowing up Descartes’ own y-axis. Poetic justice? Or ultimate folly?

Had the essential dimensional nature of numbers been recognized there would have been no need to inquire what the square root of -1 was. It would have been clear that there was no square root of -1 nor any need for such as +1 also has no square root.  As linear numbers,  neither -1 nor +1 can legitimately be said to have a square root.  Both, though, have two-dimensional analogues and these do have square roots, not recognized as such unfortunately by the mathematics hegemony.^[3]

In the next post we will look at a comparison between imaginary numbers,  which were formulated in accordance with this misconstrual about how numbers relate to dimensions,  and probable numbers which grow organically out of a consideration of how numbers and dimensions actually relate to one another in nature.^[4]  The first of these approaches can be thought of as rational planning by a central authority; the second, as the holistic manner in which nature attends to everything, all at once, and without rational forethought.

(continuedhere)

Image: A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions  (A tesseract).  There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion. By NerdBoy1392 (Own work) [CC BY-SA 3.0orGFDL],via Wikimedia Commons

Notes

[1] See the series of about nine posts that begins here.

[2] The Rationalists missed here a golden opportunity to relate number and dimension by defining square root much too narrowly. They seem to have been so mesmerized by their algebraic equations that they failed to pursue the search into deeper significance pertaining to essential linkages between dimension and number that intuition and imagination might have bestowed.

[3] As Shakespeare correctly pointed out, a rose by any name would smell as sweet. Plus one times plus one certainly equals plus one but that has nothing to do with actual square root really, just with algebraic linear multiplication.  Note has often been made in these pages of the difference between mathematical truth and scientific truth. Whereas mathematics demands only adherence to its axioms and consistency,  science requires empirical proof.  Mathematics defined square root in a certain manner centuries ago, and has since been devoutly consistent in its adherence to that definition.  In so doing it has preserved a cherished doctrine of mathematical truth, as though in formaldehyde.  It has also for many centuries contrived to be consistently scientifically incorrect.  The problem lies in the fact it has converted physicists and near everyone else to its own insular worldview.

[4] For an early discussion of the probable plane, potential dimensions, and probable numbers see here.