#coordinates
Quantum Naughts and Crosses Revisited - VIII
The Cube Sliced and Diced
Transliteration Series: Section FH(n)


(continued from here)
We come now to the Taoist/Cartesian transliteration sections of the three-dimensional cube.[1] The frontal FH section seen below is the Cartesian xy-plane we’re all familiar with from the 2-dimensional version of the Cartesian coordinate system with the third Cartesian dimension (z) added to the labeling of points. This gives us nine distinct Cartesian triad points: four vertices, four edge centers, and one face center. For all of the points, the third Cartesian dimension (z) is constant in this slice, and the vector value is positive (located toward the viewer with respect to the z=0 value of the z-axis or FHE plane which we’ll be viewing in a future post.)
The diagram shown here relates changing and unchanging trigrams of the I Ching to corresponding Cartesian ordered triads. Descartes views each of his ordered triads as referring to a single point having substantive reality in Cartesian geometric space. The I Ching and mandalic geometry, on the other hand, regard the trigrams as evanescent composite states of being in a spacetime which is ever-changing. They are relational elements in some ways analagous to the subatomic entities of particle physics.
Accordingly, it should be further understood each “point” here, though shown as a flat “square”, has a third dimension implied, and is therefore actually a “cube”, only one face of which is seen.[2] Mandalic geometry considers the point a fictional device which actually refers to a common intersection of three or more planes in a three-dimensional context, or two or more lines in a two-dimensional context. Moreover, mandalic geometry is a discretized geometry, and the trigram must be considered as having a distributed domain of action. This is illustrated in all the Cartesian transliteration points by distributing eight copies of trigrams with appropriate changing and unchanging lines among eight vertex-analogues of each Cartesian point.
The key to labeling of points in this section[3] and all those to follow can be found here. Additionally, by tradition, adding an “x” to a yin line indicates it is a changing line and adding an “o” to a yang line indicates it is a changing line. A changing yin line is considered an old yin line which is changing to a yang line; a changing yang line, an old yang line that is changing to a yinline.
Vector addition of two or more yinlines yields a yin line as result. Vector addition of two or more yang lines gives a yang line as the result. Vector addition of an unequal number of yin lines and yang lines yields as result that vector (yinoryang) in excess. Vector addition of an equal number of yin lines and yang lines gives as result Cartesian zero which, in mandalic systematics is to be considered a vector (direction) rather than a scalar (magnitude). This goes far in explaining how the I Ching and Taoism managed without an explicit zero.
Thezero was implicit or understood without using a special symbol of designation. Moreover, it was conceived as representative of an order of reality entirely different from that distinguished by the Western zero. It is, however, fully commensurate with Cartesian coordinate dynamics. It is this alternative zero, with its extraordinary capacities, that provides access to potential dimensions and to different amplitudes of dimension. This will be further elaborated in a future post where we will address how Boolean logic impacts what we’ve covered here.
For now simply note that the changing yin Line and changing yang Line in the horizontal first dimension (x) in each “point” shown in the middle column add to zero, not the zero of scalar magnitude though, but the zero of vector equilibrium.

Section FH(n)
In this section of the cube, as in all frontal sections, the third Line/dimension (z) never changes; the second Line/dimension (y) changes only in columns, as one progresses up or down; the first Line/dimension changes only in the rows, progressing left or right. This is just a consequence of viewing a two-dimensional Cartesian
xy-plane in context of a section of the three-dimensional Cartesian
xyz-cube. Although not the manner in which we are accustomed to viewing the plane, it is nonetheless fully compatible with ordinary Cartesian coordinates. It is simply an alternative perspective, one more suited for analysis/demonstration of trigram relationships in a Cartesian setting.
(continuedhere)
Notes
[1] This should be viewed as a work in progress. I’m still feeling my way with this so the content and/or format may change in the future. What is demonstrated here does not yet take into account the manner in which Boolean logic relates to the distribution of changing and unchanging trigrams nor does this series of cube sections include the all-important geometric method of composite dimension. As described, this is simply a Taoist notation transliteration of Cartesian coordinate structure. The meat and potatoes of the matter is yet to come. Of particular note here, though, is the fact that even at this early stage of translation to a version of mandalic geometry that can be considered comprehensive, what is possibly best described as a decussationbetweenyinandyang lines is already evident at every Cartesian triad point containing a “Cartesian zero”. Worth mentioning here, this will be a key feature addressed in future posts.
[2]Point, square, and cube, have all been placed in quotation marks to indicate that what is being referred to here is actually a different category of objects or elements which should in some sense be understood as relating to fractals or fractal structure and of a different dimensionality entirely than are those ordinary geometric objects. The admittedly deficient terminology used here is necessitated by the fact that sufficiently appropriate vocabulary terms to describe the reality intended do not currently exist, or if they do are not as yet known to me. Since we are representing a Cartesian point (ordered triad) as a quasi-cubic structure here, it must have a near face (n) and a far face (f) in each section with respect to the viewer. The chart displayed details the near face (n) of Section FH.
[3] This is the frontal section through the cube nearest a viewer. It is Descartes’ xy-plane with label of the third dimension (z) added so each point label shown is a Cartesian ordered triad rather than an ordered pair as textbooks generally show the plane. Why the difference? Because the geometry texts are interested only in demonstrating the two-dimensional plane in isolation, whereas we want to see it as it exists in the context of three or more dimensions. Cartesian triads are shown by convention as (x,y,z), so the xy-plane emerges from the first two coordinates of the points in this section, and all the z-coordinates seen here are positive (+1). The FE plane has all of its x and y coordinates identical to those seen here but its z-coordinates are all negative (-1). The FHE plane has all the x and y coordinates identical to those seen here but its z-coordinates are all zero (0).
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 296-
Quantum Naughts and Crosses Revisited - I

(continued from here)
Because nature is ever playful, grokking mandalic geometry is much like a game. We view it as a largely serious one, though, one that involves combinatorics, Boolean logic, and magic squares and cubes. Groundwork for what appears in this post, and several to follow, was laid in May, 2014 in a series titled “Quantum Naughts and Crosses” which began here.
The game is played on a board or field made of three-dimensional coordinates of the Cartesian variety upon which are superimposed the six additional extraordinary dimensions unique to mandalic coordinates. For convenience and ease of representation, the board will be displayed here in two dimensional sections abstracted from the Cartesian cube and from the superimposed mandalic hypercube in a manner analogous to the way computed tomography renders sections of the human body.
The sections commonly used[1] in computed tomographyandmagnetic resonance imaging (MRI) are
- Frontal
- Transverse
- Sagittal
For our purposes here, these can be thought of as
- Planes perpendicular to the z-axis viewed from front to back of cube
- Planes perpendicular to the y-axis viewed from top to bottom of cube
- Planes perpendicular to the x-axis viewed from side right to left of cube
These “cuts” will produce square sections through xy-, xz-, and yz-planes, respectively, of the Cartesian cube and, in the case of the mandalic cube, analogous sections of higher dimension.
These choices of sections are made largely for convenience and ease of communicability. They are mainly of a conventional nature.[2] On the other hand, there is special significance in the fact that all three section types progress from identity faces of the cube, containing the trigram or hexagram HEAVEN, to inversion faces, containing trigram or hexagram EARTH. Some manner of consistency of this sort is necessary. The one chosen here will make things easier as we progress.
Ourgameboard has 27 discretized Cartesian points, centered in 3 amplitude levels about the Cartesian origin (0,0,0).[3] Each point in the figure on the right above is represented by a single small cube, but in the two-dimensional sections we’ll be using for elaboration, they will appear as small squares. So the gameboard is “composed of” 27 cubes arranged in a 3x3x3 pattern. But in descriptions of sections, we will view 9 squares in a 3x3 pattern. This configuration will appear as

But keep in mind each small square in this figure is actually a small cube representing one of the 27 discretized Cartesian points we’ve described.
Until next time, then.
(continuedhere)
Notes
[1] The origin of the word "tomography" is from the Greek word “tomos” meaning “slice” or “section” and “graphe” meaning “drawing.” A CT imaging system produces cross-sectional images or “slices” of anatomy, like the slices in a loaf of bread. The “slices” made are transverse (cross-sections from head to toes or, more often, a portion thereof), but reconstructions of the other types of sections described above are sometimes made, and MRI generates all three types natively.
[2] Admittedly, I’ve chosen the convention here myself and to date it is shared by no one else. Perhaps at some future time it will be a shared convention. One can only hope.
[3] These three discrete amplitude levels of potentiality in the mandalic 9-cube correspond geometrically to face centers, edge centers and vertices of the 3-cube of Cartesian coordinates. They are encoded by the six new potential dimensions interacting with the three ordinary Cartesian dimensions in context of the hybrid 6D/3D mandalic cube. They are a feature of the manner of interaction of all nine temporospatial dimensions acting together in holistic fashion. This should begin to give an idea why there is no Taoist line that can generate a 9-cube in a fashion analogous to the way the Western number line is used to generate the Cartesian / Euclidean 3-cube. The 9-dimensional entity is primeval and a variety of different types of "line" can be derived from it. Similarly, the mandala of the I Ching hexagrams cannot be derived from the logic encoded in any linear structure. An overarching perspective is required to derive first the mandala of hexagrams and then from it, a variety of Taoist line types. Nature may be playful, but it is not nearly as simplistic as our Western science, mathematics, and philosophy would have it.
© 2015 Martin Hauser
Please note: The content and/or format of this post may not be in finalized form. Reblog as a TEXT post will contain this caveat alerting readers to refer to the current version in the source blog. A LINK post will itself do the same. :)
Scroll to bottom for links to Previous / Next pages (if existent). This blog builds on what came before so the best way to follow it is chronologically. Tumblr doesn’t make that easy to do. Since the most recent page is reckoned as Page 1 the number of the actual Page 1 continually changes as new posts are added. To determine the number currently needed to locate Page 1 go to the most recent post which is here. The current total number of pages in the blog will be found at the bottom. The true Page 1 can be reached by changing the web address mandalicgeometry.tumblr.com to mandalicgeometry.tumblr.com/page/x, exchanging my current page number for x and entering. To find a different true page(p) subtract p from x+1 to get the number(n) to use. Place n in the URL instead of x (mandalicgeometry.tumblr.com/page/n) where
n = x + 1 - p. :)
-Page 286-
This was the first gift accepted by the Museum.
The back and cover of this sarcophagus are unfinished, and its inscription tablet is blank, which may imply that it went unsold in antiquity. Garlands of oak leaves supported by two erotes and four Victories adorn the front and sides. Medusa heads fill the spaces above the garlands, except in the center of the front, where there is the blank inscription tablet. Six erotes hunt various wild animals along the front face of the cover, while two others stand at the corners. On the left end, Eros awakens Psyche with an arrow, and on the right, they embrace.
Post link



If I had a billion dollars, this would be my outfit for 2 out of 3 days of EDC. Possibly all 3.
The Mimpi Fairy Bikini Top: Jackalope Land, $92
The Mimpi Fairy Ruffle Bikini Bottoms: Jackalope Land, $92
The Mimpi Dream Catcher Gloves: Jackalope Land, $104
The Mimpi Dreamer Ankle Boots: Jackalope Land, $530
When describing the trajectory of a point particle in space, we can use simple kinematic physics to describe properties of the particle: force,energy, momentum, and so forth. But are there useful measures we can use to describe the qualities of the trajectory itself?
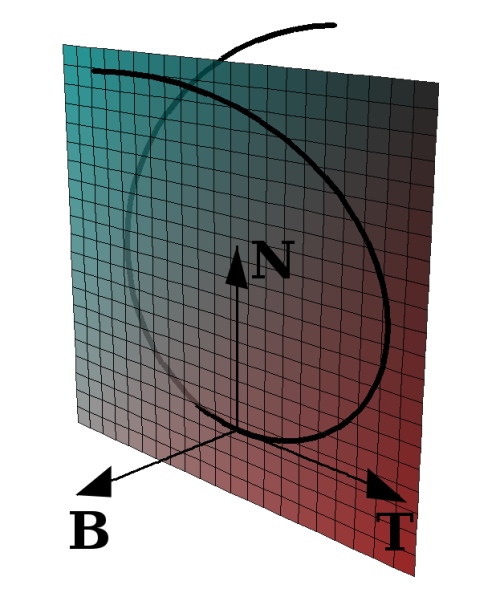
Enter the Frenet-Serret (or TNB) frame. In this post, we’ll show how to construct three (intuitively meaningful) orthonormal vectors that follow a particle in its trajectory. These vectors will be subject to the Frenet-Serret equations, and will also end up giving us a useful way to interpret curvature and torsion.
First, we define arc length: let s(t) = ∫0t||x’(τ)|| dτ. (We give a quick overview of integration in this post.) If you haven’t encountered this definition before, don’t fret: we’re simply multiplying the change in position of the particle x’(τ) by the small time step dτ summed over every infinitesimal time step from τ=0 to τ=t=”current time”. The post linked to above also explains a short theorem that may illustrate this point more lucidly.
Now, consider a particle’s trajectory x(t). What’s the velocity of this particle? Its speed, surely, is ds/dt: the change in arc length (distance traveled) over time. But velocity is a vector, and needs a direction. Thus we define the velocity v=(dx/ds)⋅(ds/dt). This simplifies to the more obvious definition dx/dt, but allows us to separate out the latter term as speed and the former term as direction. This first term, dx/ds, describes the change in the position given a change in distance traveled. As long as the trajectory of the particle has certain nice mathematical properties (like smoothness), this vector will always be tangent to the trajectory of the particle. Think of this vector like the hood of your car: even though the car can turn, the hood will always point in whatever direction you’re going towards. This vector T ≡ dx/ds is called the unit tangent vector.
We now define two other useful vectors. The normal vector: N ≡ (dT/ds) / ( |dT/ds| ) is a vector of unit length that always points in whichever way T is turning toward. It can be shown — but not here — that T⊥N. The binormal vector B is normal to both TandN; it’s defined as B≡TxN. So T, N, and B all have unit length and are all orthogonal to each other. Since T depends directly on the movement of the particle, N and B do as well; therefore, as the particle moves around, the coordinate system defined by T, N, and B moves around as well, connected to the particle. The frame is always orthonormal and always maintains certain relationships to the particle’s motion, so it can be useful to make some statements in the context of the TNB frame.
The Frenet-Serret equations, as promised:
- dT/ds = κN
- dN/ds = -κT + τB
- dB/ds = -τN
Here, κ is the curvature and τ is the torsion. Further reading (lookup the Darboux vector) illustrates that κ represents the rotation of the entire TNB frame about the binormal vector B, and τ represents the rotation of the frame about T. The idea of the particle trajectory twisting and rolling nicely matches the idea of what it might be like to be in the cockpit of one of these point particles, but takes this depth of vector analysis to get to.
Bonus points: remember how v=Tv, with v the speed? Differentiate this with respect to time, play around with some algebra, and see if you can arrive at the following result: the acceleration a = κv2N + (d2s/dt2)T. Thoughtful consideration will reveal the latter term as the tangential acceleration, and knowing that 1/κ ≡ ρ = “the radius of curvature” reveals that the first term is centripetal acceleration.
—
Photo credit: Salix albaaten.wikipedia
Post link